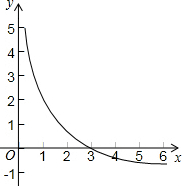
小颖画了一个函数y=$\frac{a}{x}$-1的图象如图.那么关于x的分式方程$\frac{a}{x}$=1的解是( )A．x=1B．x=2C．x=3D．x=4 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

18．

小颖画了一个函数y=$\frac{a}{x}$-1的图象如图，那么关于x的分式方程$\frac{a}{x}$=1的解是（　　）

A．

x=1

B．

x=2

C．

x=3

D．

x=4

分析根据函数与方程的关系，可得答案．

解答解：由函数y=$\frac{a}{x}$-1的图象，得
分式方程$\frac{a}{x}$=1的解是x=3．
故选：C．

点评本题考查了反比例函数图象，利用了函数图象与x轴的交点的横坐标是相应方程的解．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

8．

如图，AB为⊙O的弦，△ABC的两边BC、AC分别交⊙O于D、E两点，其中∠B=60°，∠EDC=70°，则∠C=50度．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．

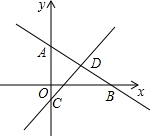如图，过点A（0，2），B（3，0）的直线AB与直线CD：y=$\frac{5}{6}x$-1交于点D，C为直线y轴的交点．
（1）求直线AB的解析式；
（2）求S_△ADC．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

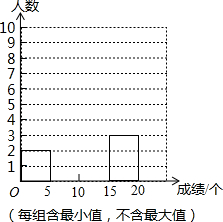某校为了解九年级300名男生的体能情况，随机抽取了部分九年级男生进行“引体向上”测试，这些男生的测试成绩（单位：个）如下：
9，12，3，13，18，8，8，4，10，12，13，■，9，8，12，13，18，13，12，10．
其中有一数据被污损，统计员只记得这组数据的平均数是11．
（1）求该组样本数据中被污损的数据和这组数据的众数；
（2）请补充完整如图所示的频数分布直方图；
（3）若规定完成10个以上（含10个）为体能达标，则估计该校九年级男生中有多少人体能达标？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．

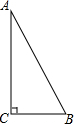如图，△ABC是直角三角形，∠ACB=90°．
（1）动手操作：利用尺规作∠ABC的平分线，交AC于点O，再以O为圆心，OC的长为半径作⊙O（保留作图痕迹，不写作法）；
（2）综合运用：在你所作的图中，
①判断AB与⊙O的位置关系，并证明你的结论；
②若AC=12，tan∠OBC=$\frac{2}{3}$，求⊙O的半径．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．如图，在平面直角坐标系xOy中，函数y=ax²+bx+1（a≠0）的图象与x的正半轴交于点A，与x的负半轴交于点B，与y轴交于点C．△PAC中，P（1，-1），∠P=90°，PA=PC．
（1）求点A的坐标．
（2）将△PAC沿AC翻折，若点P的对应点Q恰好落在函数y=ax²+bx+1（a≠0）的图象上，求a与b的值．
（3）将△ACO绕点A逆时针旋转90°得到△ADE，在x轴上取一点M，将∠PMD沿PM翻折，若点D的对应点F恰好落在x轴上，求点M的坐标．

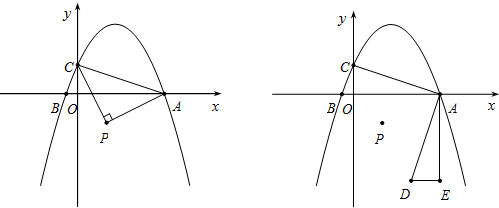
查看答案和解析>>

科目：初中数学 来源： 题型：选择题

10．

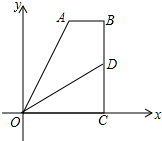已知如图，在平面直角坐标系中，四边形ABCD的顶点A，B在第一象限，AB∥x轴，∠B=90°，AB+OC=OA，OD平分∠AOC交BC于点D．若四边形ABDO的面积为4，反比例函数y=$\frac{k}{x}$的图象经过点D，点A，则k的值是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．如图1，在矩形ABCD中，AB=4cm，BC=8cm．E，F，G，H分别是AB，BC，CD，DA的中点，连结EF，FG，GH，HE．
（1）求证：四边形EFGH是菱形；
（2）如图2，若E₁，E₂分别从E出发以1cm/s的速度沿射线EA，EB方向运动，同时G₁，G₂从G出发以同样的速度分别沿射线GD，GC方向运动，E₁F与E₂H交于点M，G₁F与G₂H交于点N．设运动的时间为t（s），求四边形E₁FG₂H与四边形E₂HG₁F覆盖平面的总面积y与运动时间t之间的函数关系式；
（3）当t为何值时，四边形HMFN为正方形．