
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
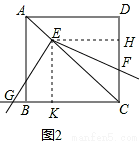
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,情给予证明;若不成立,请说明理由;
(1)证明见解析;(2)是,证明见解析.
【解析】
试题分析:(1)由四边形ABCD是正方形,点E与点A重合,易证得ED=EB,∠D=∠EBG=90°,又由∠GEF=90°,利用同角的余角相等,即可得∠BEG=∠DEF,然后利用ASA即可判定△BEG≌△DEF,则可证得EF=EG;
(2)首先过点E作EH⊥CD于H,作EK⊥BC于K,易证得四边形EKCH是正方形,同(1)即可证得△GEK≌△FEH,证得EF=EG.
试题解析:(1)证明:∵四边形ABCD是正方形,点E与点A重合,
∴ED=EB,∠D=∠EBG=90°,
∵∠GEF=90°,
∴∠BEG+∠BEF=∠BEF+∠DEF=90°,
∴∠BEG=∠DEF,
在△BEG和△DEF中,
 ,
,
∴△BEG≌△DEF(ASA),
∴EF=EG;
(2)成立.理由:
【解析】
过点E作EH⊥CD于H,作EK⊥BC于K,
∴∠EHC=∠EKC=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠HCE=45°,
∴四边形EKCH是矩形,∠HEC=∠HCE=45°,
∴EH=CH,
∴四边形EKCH是正方形,
∴EH=EK,∠EHF=∠EKG=90°,
∵∠GEF=90°,
∴∠GEK+∠KEF=∠KEF+∠FEH=90°,
∴∠GEK=∠FEH,
在△GEK和△FEH中,
 ,
,
∴△GEK≌△FEH(ASA),
∴EF=EG.
考点:1.正方形的性质;2.全等三角形的判定与性质.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:2014-2015学年福建省泉州市泉港区八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在正方形ABC1D1中,AB=1.连接AC1,以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.则
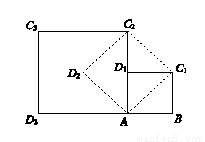
(1)第三个正方形AC2C3D3的边长为__________;
(2)按此规律所作的第7个正方形的面积为__________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级12月月考数学试卷(解析版) 题型:选择题
二次函数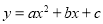 的部分对应值如下表:
的部分对应值如下表:
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
下面关于二次函数及其图象说法不正确的是( )
A.对称轴为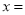 1
1
B.y的最大值是-9
C.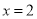 对应的函数值
对应的函数值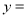 -8
-8
D.抛物线截x轴所得的线段长是6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上数学期末模拟数学试卷(解析版) 题型:解答题
如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,画∠MAB、∠NBA的平分线交于E,按下列要求回答:
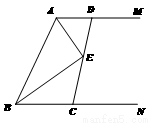
(1)∠AEB是什么角?并说明理由。
(2)过点E作一直线交AM于D,交BN于C,观察线段DE、CE,你有何发现?
(3)无论DC的两端点在AM、BN如何移动,只要DC经过点E,①AD+BC=AB;②AD+BC=CD谁成立?并说明理由
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安市毕业生学业水平模拟二数学试卷(解析版) 题型:填空题
“上升数”是一个数中右边数字比左边数字大的自然数(如:34,568,2469等).任取一个两位数,是 “上升数”的概率是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古化德县第三中学九年级上学期期末测试数学试卷(解析版) 题型:选择题
如图所示,随机闭合开关K1,K2,K3中的两个,则能让两盏灯泡同时发光的概率为( )
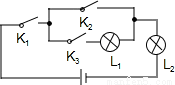
A.1 B.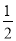 C.
C.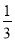 D.
D.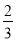
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com