
如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,画∠MAB、∠NBA的平分线交于E,按下列要求回答:
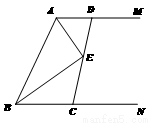
(1)∠AEB是什么角?并说明理由。
(2)过点E作一直线交AM于D,交BN于C,观察线段DE、CE,你有何发现?
(3)无论DC的两端点在AM、BN如何移动,只要DC经过点E,①AD+BC=AB;②AD+BC=CD谁成立?并说明理由
∠AEB为直角;理由见解析;(2)ED=EC;(3)AD+BC=AB.理由见解析.
【解析】
试题分析:(1)由两直线平行同旁内角互补,及角平分线的性质不难得出∠1+∠3=90°,再由三角形内角和等于180°,即可得出∠AEB是直角的结论;
(2)过E点作辅助线EF使其平行于AM,由平行线的性质可得出各角之间的关系,进一步求出边之间的关系;
(3)由(2)中得出的结论可知EF为梯形ABCD的中位线,可知无论DC的两端点在AM、BN如何移动,只要DC经过点E,AD+BC的值总为一定值.
试题解析:(1)∵AM∥BN,
∴∠MAB+∠ABN=180°,
又AE,BE分别为∠MAB、∠NBA的平分线,
∴∠1+∠3=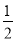 (∠MAB+∠ABN)=90°,
(∠MAB+∠ABN)=90°,
∴∠AEB=180°-∠1-∠3=90°,
即∠AEB为直角;
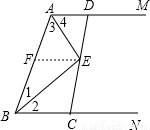
(2)过E点作辅助线EF使其平行于AM,
∵AM∥BN,EF∥BC,
∴EF∥AD∥BC,
∴∠AEF=∠4,∠BEF=∠2,
∵∠3=∠4,∠1=∠2,
∴∠AEF=∠3,∠BEF=∠1,
∴AF=FE=FB,
∴F为AB的中点,又EF∥AD∥BC,
根据平行线等分线段定理得到E为DC中点,
∴ED=EC;
(3)由(2)中结论可知,无论DC的两端点在AM、BN如何移动,只要DC经过点E,
总满足EF为梯形ABCD中位线的条件,所以总有AD+BC=2EF=AB.
考点:1.梯形中位线定理;2.平行线的性质;3.三角形内角和定理;4.等腰三角形的性质.


科目:初中数学 来源:2014-2015学年四川省九年级12月月考数学试卷(解析版) 题型:解答题
(10分)如图,O是坐标原点,直线OA与双曲线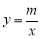 在第一象限内交于点A,过点A的直线
在第一象限内交于点A,过点A的直线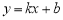 与x轴正半轴交于点B,与双曲线的另一交点为C,连结OC. 若
与x轴正半轴交于点B,与双曲线的另一交点为C,连结OC. 若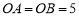 ,
,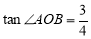 .
.
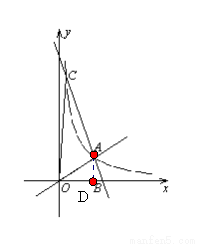
(1)求双曲线和直线AB的解析式;
(2)求△AOC的面积.
(3)在第一象限内,根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级12月月考数学试卷(解析版) 题型:选择题
下列命题,真命题( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形
D.平分弦的直径垂直于这条弦
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上数学期末模拟数学试卷(解析版) 题型:计算题
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,情给予证明;若不成立,请说明理由;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上数学期末模拟数学试卷(解析版) 题型:填空题
一个几何体是由一些大小相同的小正方体摆成的,其主视图与左视图如图所示,则组成这个几何体的小正方体最少有 个
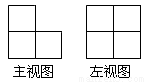
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上数学期末模拟数学试卷(解析版) 题型:选择题
如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
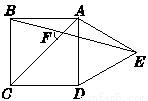
A.45? B.55? C.60? D.75?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安市毕业生学业水平模拟二数学试卷(解析版) 题型:选择题
把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A. 1<m<7 B. 3<m<4 C. m>1 D. m<4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古化德县第三中学九年级上学期期末测试数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2a;④am2+bm+>0(m≠-1).其中正确的个数是
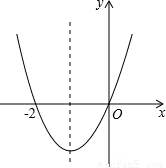
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com