
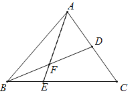
【题目】如图,在![]() 中,
中,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 交于点
交于点![]() ,
,![]() .若
.若![]() 的面积为18,给出下列命题:①
的面积为18,给出下列命题:①![]() 的面积为16;②
的面积为16;②![]() 的面积和四边形
的面积和四边形![]() 的面积相等;③点
的面积相等;③点![]() 是
是![]() 的中点;④四边形
的中点;④四边形![]() 的面积为
的面积为![]() ;其中,正确的结论有_____________.
;其中,正确的结论有_____________.
【答案】③④
【解析】
①根据等高的三角形面积比等于底边比即可求解;②先分别得出△ABE的面积与△BCD的面积的关系,然后进一步求解即可;③过点D作DG∥BC,通过三角形中位线性质以及全等三角形的判定和性质进一步求解即可;④根据题意将该四边形面积计算出来即可.据此选出正确的选项从而得出答案.
① ∵![]() ,
,
∴EB=![]() BC,
BC,
∴![]() 的面积=
的面积=![]() ,
,
故①错误;
② ∵![]() ,点D为AC的中点,
,点D为AC的中点,
∴△ABE的面积≠△BCD的面积,
∴![]() 的面积和四边形
的面积和四边形![]() 的面积不相等,
的面积不相等,
故②错误;
③ 如图,过点D作DG∥BC,
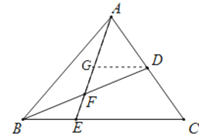
∵D是AC中点,DG∥BC,
∴DG=![]() ,
,
∵![]() ,
,
∴DG=EB,
∵DG∥BC,
∴∠DGF=∠BEF,∠GDF=∠EBF,
在△DGF与△BEF中,
∵∠DGF=∠BEF,DG=EB,∠GDF=∠EBF,
∴△DGF≌△BEF(ASA),
∴DF=BF,
∴点![]() 是
是![]() 的中点,
的中点,
故③正确;
④ 四边形![]() 的面积=
的面积=![]() ,
,
故④正确;
综上所述,正确的结论有:③④,
故答案为:③④.


科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=8,BC=6,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、ND,则图中阴影部分的面积之和等于_____.
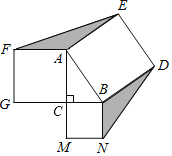
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
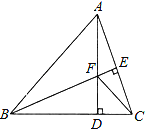
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2![]() ,则线段CD的长是( )
,则线段CD的长是( )
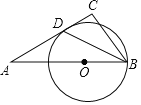
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
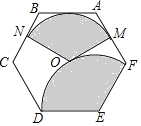
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=2cm,BC=3cm,点P沿B→A→D运动,运动到点D时停止运动,点P运动的同时,另一点Q从B→C运动,速度是点P的一半,当点P停止运动时,点Q也停止运动.设点P运动的路程为xcm,其中设![]() ,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.
,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.
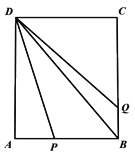
(1)如图是画出的函数![]() 与x的函数图象,观察图象.当x=1时,
与x的函数图象,观察图象.当x=1时,![]() =_____;并写出函数的一条性质:________________________________________.
=_____;并写出函数的一条性质:________________________________________.
(2)请帮助可可写出![]() 与x的函数关系式(不用写出取值范围)__________________.
与x的函数关系式(不用写出取值范围)__________________.
(3)请按照列表、描点、连线的步骤在同一直角坐标系中,画出函数![]() 的图象.
的图象.
(4)结合画出函数图象,解决问题:当![]() 时,点P运动的路程x=_______.
时,点P运动的路程x=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com