
【题目】已知,BC∥OA,∠B=∠A=108°,试解答下列问题:
(1)如图1所示,则∠O= °,并判断OB与AC平行吗?为什么?
(2)如图2,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于 °;
(3)在第(2)题的条件下,若平行移动AC,如图3.
①求∠OCB:∠OFB的值;
②当∠OEB=∠OCA时,求∠OCA的度数(直接写出答案,不必写出解答过程).

【答案】(1)72,OB∥AC,见解析;(2)40;(3)①∠OCB:∠OFB=1:2;②∠OCA=54°
【解析】
(1)首先根据平行线的性质可得∠B+∠O=180![]() ,再根据∠A=∠B可得∠A+∠O=180
,再根据∠A=∠B可得∠A+∠O=180![]() ,进而得到OB∥AC;
,进而得到OB∥AC;
(2)根据角平分线的性质可得∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,进而得到∠EOC=
∠FOA,进而得到∠EOC=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ∠BOA=40
∠BOA=40![]() ;
;
(3)①由BC∥OA可得∠FCO=∠COA,进而得到∠FOC=∠FCO,故∠OFB=∠FOC+∠FCO=2∠OCB,进而得到∠OCB:∠OFB=1:2;
②由(1)知:OB∥AC,BC∥OA,得到∠OCA=∠BOC,∠OEB=∠EOA,根据(1)、(2)的结果求得.
解:(1)∵BC∥OA,∠B=108![]()
∴∠O=180![]() -108
-108![]() =72
=72![]() ,
,
∵BC∥OA,
∴∠B+∠O=180![]() ,
,
∵∠A=∠B
∴∠A+∠O=180![]() ,
,
∴OB∥AC
故答案为:72![]() ;
;
(2)∵∠A=∠B=108![]() ,由(1)得∠BOA=180
,由(1)得∠BOA=180![]() ﹣∠B=72
﹣∠B=72![]() ,
,
∵∠FOC=∠AOC,并且OE平分∠BOF,
∴∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,
∠FOA,
∴∠EOC=∠EOF+∠FOC=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ∠BOA=36
∠BOA=36![]()
故答案为:36![]() ;
;
(3)①∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
②由(1)知:OB∥AC,∴∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
∴∠OCA=∠BOC=2α+β
由(1)知:BC∥OA,
∴∠OEB=∠EOA=α+β+β=α+2β
∵∠OEB=∠OCA
∴2α+β=α+2β
∴α=β
∵∠AOB=72![]() ,
,
∴α=β=18![]()
∴∠OCA=2α+β=36![]() +18
+18![]() =54
=54![]() .
.


科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
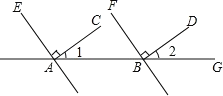
【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松桃孟溪火车站一检修员某天乘一辆检修车在笔直的铁轨上来回检修,规定向东为正,从车站出发到收工时,行走记录为(单位:千米):+15,-2,-5,-1,+10,-3,-2,-12,+4,+6.
⑴计算收工时,检修员在车站的哪一边,此时,距车站多远?
⑵若汽车每千米耗油0.1升,且汽油的价格为每升6.8元,求这一天检修员从出发到收工时所耗油费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提倡节约用水,我县自来水公司每月只给某单位计划内用水200吨,计划内用水每吨收费2.4元,超计划部分每吨按3.6元收费.
⑴用代数式表示下列问题(最后结果需化简 ):设用水量为![]() 吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?
吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?
⑵若某单位4月份缴纳水费840元,则该单位用水量多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长是1,点E是CD边上的中点.P为正方形ABCD边上的一个动点,动点P从A点出发,沿![]() 运动,到达点E.若点P经过的路程为自变量x,
运动,到达点E.若点P经过的路程为自变量x,![]() 的面积为因变量y,则当
的面积为因变量y,则当![]() 时,x的值等于_________.
时,x的值等于_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
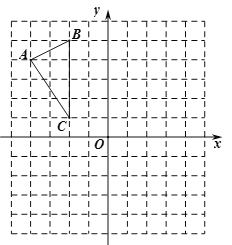
【题目】如图,![]() 在平面直角坐标系内,顶点的坐标分别为
在平面直角坐标系内,顶点的坐标分别为![]() ,
,![]() 、
、![]() .
.
(1)平移![]() ,使点
,使点![]() 移到点
移到点![]() ,画出平移后的
,画出平移后的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(2)将![]() 绕点
绕点![]() 旋转
旋转![]() ,得到
,得到![]() ,画出旋转后的
,画出旋转后的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(3)求(2)中的点![]() 旋转到点
旋转到点![]() 时,点
时,点![]() 经过的路径长(结果保留
经过的路径长(结果保留![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com