
【题目】阅读下面材料:点A、B在数轴上分别表示实数a、b,A,B两点之间的距离表示为│AB│.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|ab|;
![]()
当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边,|AB|=|OB||OA|=|b||a|=ba=|ab|;
②如图3,点A、B都在原点的左边,|AB|=|OB||OA|=|b||a|=b(a)=ab=│a-b│;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|b|+|a|=-b+a=|ab|;综上,数轴上A、B两点之间的距离|AB|=|ab|.
(1)回答下列问题:
①数轴上表示3和9的两点之间的距离是______,数轴上表示5和9的两点之间的距离是______,数轴上表示10和3的两点之间的距离是______;
②数轴上表示x和4的两点A和B之间的距离为______,如果|AB|=6,那么x为______;
③当代数式|x+2|+|x3|取最小值______时,相应的x的取值范围是______.
(2)a、b在数轴上位置如图所示,请化简式子│a+1│-│2b-2│-│a+b│
![]()
【答案】(1)①6,4,13;②![]() ,2或-10;③5,-2≤x≤3;(2)3b-3.
,2或-10;③5,-2≤x≤3;(2)3b-3.
【解析】
(1)①根据数轴上A、B两点之间的距离|AB|=|ab|即可得答案;②根据数轴上两点间的距离公式解答即可;③|x+2|+|x3|可表示某点到表示-2和3的点的距离的和,可得这一点表示的数在-2和3之间时,|x+2|+|x3|取最小值,根据绝对值的性质化简即可得答案;(2)由数轴可得a<-1,0<b<1,即可判断a+1、2b-2、a+b的符号,根据绝对值的性质化简即可得答案.
(1)①数轴上表示3和9的两点之间的距离是![]() =6,
=6,
数轴上表示5和9的两点之间的距离是![]() =4,
=4,
数轴上表示10和3的两点之间的距离是![]() =13,
=13,
故答案为:6,4,13
②数轴上表示x和4的两点A和B之间的距离为![]() =
=![]() ,
,
∵![]() =6,
=6,
∴x+4=6或x+4=-6,
∴x=2或x=-10,
故答案为:![]() ,2或-10
,2或-10
③∵代数式|x+2|+|x-3|可看作数轴上某点到表示-2和3的点的距离之和,
∴当该点表示的数在-2和3之间时,|x+1|+|x+2|取最小值.
∴-2≤x≤3.
∴x+2≥0,x-3≤0,
∴|x+2|+|x-3|=x+2-(x-3)=x+2-x+3=5
∴当代数式|x+2|+|x3|取最小值5时,相应的x的取值范围是-2≤x≤3.
故答案为:5,-2≤x≤3
(2)由数轴可知a<-1,0<b<1,
∴a+1<0,b-1<0,a+b<0,
∴│a+1│-│2b-2│-│a+b│
=-(a+1)+(2b-2)+(a+b)
=3b-3.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解(solution).已知:关于![]() 的方程
的方程![]() .
.
(1)若![]() 是方程
是方程![]() 的解,求
的解,求![]() 的值;
的值;
(2)若关于![]() 的方程
的方程![]() 的解比方程
的解比方程![]() 的解大6,求
的解大6,求![]() 的值;
的值;
(3)若关于![]() 的方程
的方程![]() 与
与![]() 均无解,求代数式
均无解,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位假日组织员工到A地旅游,现雇一辆载19人(不能超载)的客车,而到A地旅游有甲、乙两条路可走。有关数据如下:

(1)设y![]() ,y
,y![]() (元)分别表示客车走甲、乙两条路线司机的收入,求y
(元)分别表示客车走甲、乙两条路线司机的收入,求y![]() ,y
,y![]() 与乘客人数x(人)的关系式;
与乘客人数x(人)的关系式;
(2)通过以上情况分析,你若是司机,应该选择那一条路线?请作出函数图象加以说明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为(_______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.


(1)求证:BF=DF;
(2)如图2,过点D作DG∥BE交BC于点G,连接FG交BD于点O,若AB=6,AD=8,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )

A.  B.
B. 
C. 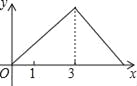 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
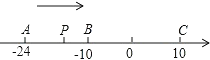
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA=________,PC=________;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com