
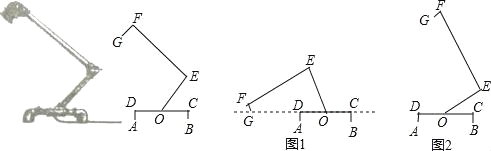
【题目】小华在“科技创新大赛”中制作了一个创意台灯作品,现忽略支管的粗细,得到它的侧面简化结构图如图所示.已知台灯底部支架CD平行于水平面,FE⊥OE,GF⊥EF,台灯上部可绕点O旋转,OE=20cm,EF=20![]() cm.
cm.
(1)如图1,若将台灯上部绕点O逆时针转动,当点G落在直线CD上时,测量得∠EOG=65°,求FG的长度(结果精确到0.1cm);
(2)将台灯由图1位置旋转到图2的位置,若此时F,O两点所在的直线恰好与CD垂直,求点F在旋转过程中所形成的弧的长度.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,![]() ≈1.73,可使用科学计算器)
≈1.73,可使用科学计算器)
【答案】(1)FG的长度约为3.8cm.
(2)![]() cm
cm
【解析】
试题分析:(1)作GM⊥OE可得矩形EFGM,设FG=xcm,可知EF=GM=20![]() cm,OM=(20﹣x)cm,根据tan∠EOG=
cm,OM=(20﹣x)cm,根据tan∠EOG= ![]() 列方程可求得x的值;
列方程可求得x的值;
(2)RT△EFO中求出OF的长及∠EOF的度数,由∠EOG度数可得旋转角∠FOF′度数,根据弧长公式计算可得.
试题解析:(1)如图,作GM⊥OE于点M,

∵FE⊥OE,GF⊥EF,
∴四边形EFGM为矩形,
设FG=xcm,
∴EF=GM=20![]() cm,FG=EM=xcm,
cm,FG=EM=xcm,
∵OE=20cm,
∴OM=(20﹣x)cm,
在RT△OGM中,
∵∠EOG=65°,
∴tan∠EOG=![]() ,即
,即![]() =tan65°,
=tan65°,
解得:x≈3.8cm;
故FG的长度约为3.8cm.
(2)连接OF,
在RT△EFO中,∵EF=20![]() ,EO=20,
,EO=20,
∴FO=![]() =40,tan∠EOF=
=40,tan∠EOF= ![]() =
=![]() =
=![]() ,
,
∴∠EOF=60°,
∴∠FOG=∠EOG﹣∠EOF=5°,
又∵∠GOF′=90°,
∴∠FOF′=85°,
∴点F在旋转过程中所形成的弧的长度为:![]() =
=![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】![]() 与
与 ![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.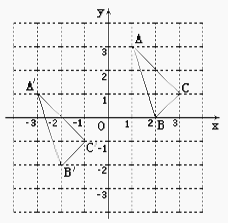
(1)分别写出下列各点的坐标:![]() ,
, ![]() ,
, ![]() ;
;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:;
经过怎样的平移得到:;
(3)若点 ![]() (
( ![]() ,
, ![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后 ![]() 内的对应点
内的对应点 ![]() 的坐标为;
的坐标为;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1
B.a=﹣5,b=1
C.a=5,b=﹣1
D.a=﹣5,b=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(﹣1,0),B(3,0),与y轴相交于点C(0,﹣3).
(1)求此二次函数的解析式.
(2)若抛物线的顶点为D,点E在抛物线上,且与点C关于抛物线的对称轴对称,直线AE交对称轴于点F,试判断四边形CDEF的形状,并说明理由.
(3)若点M在x轴上,点P在抛物线上,是否存在以A,E,M,P为顶点且以AE为一边的平行四边形?若存在,请直接写出所有满足要求的点P的坐标;若不存在,请说明理由.
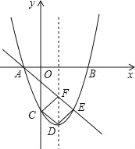
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为治理大气污染,保护人民健康.某市积极行动,调整产业结构,压减钢铁生产总量,2013年某市钢铁生产量为9700万吨,计划到2015年钢铁生产量设定为5000万吨,设该市每年钢铁生产量平均降低率为x,依题意,下面所列方程正确的是( )
A.9700(1﹣2x)=5000
B.5000(1+x)2=9700
C.5000(1﹣2x)=9700
D.9700(1﹣x)2=5000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com