
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�ڵ�A����1��0����B��3��0������y���ཻ�ڵ�C��0����3����
��1����˶��κ����Ľ���ʽ��
��2���������ߵĶ���ΪD����E���������ϣ������C���������ߵĶԳ���Գƣ�ֱ��AE���Գ����ڵ�F�����ж��ı���CDEF����״����˵�����ɣ�
��3������M��x���ϣ���P���������ϣ��Ƿ������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ������ڣ���ֱ��д����������Ҫ��ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
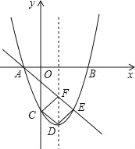
���𰸡���1�������ߵĽ���ʽΪy=x2��2x��3��
��2���ı���EFCD����������
��3����P��������1+![]() ��2����1��
��2����1��![]() ��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�
��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�
��������
�����������1�����ô���ϵ�������ɽ�����⣮
��2�������ı���EFCD�������Σ���ͼ1�У�����CE��DF���ڵ�K�����E��F��D��C�ĵ����ֻ꣬Ҫ֤��DF��CE��DF=CE��KC=KE��KF=KD����֤����
��3����ͼ2�У�������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ����ݵ�P��������Ϊ2��2�����ɽ�����⣮
�����������1����A����1��0����B��3��0����C��0����3������y=ax2+bx+c�� ��
��
���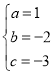 ���������ߵĽ���ʽΪy=x2��2x��3��
���������ߵĽ���ʽΪy=x2��2x��3��
��2�������ı���EFCD�������Σ�
���ɣ���ͼ1�У�����CE��DF���ڵ�K��
��y=��x��1��2��4��������D��1��4������C��E���ڶԳ���Գƣ�C��0����3����
��E��2����3������A����1��0������ֱ��AE�Ľ���ʽΪy=kx+b��
��![]() �����
�����![]() ��
��
��ֱ��AE�Ľ���ʽΪy=��x��1��
��F��1����2����
��CK=EK=1��FK=DK=1��
���ı���EFCD��ƽ���ı��Σ�
����CE��DF��CE=DF��
���ı���EFCD�������Σ�
��3����ͼ2�У�������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�

�������P��������Ϊ2��2��
��y=2ʱ��x2��2x��3=2�����x=1��![]() ��
��
�ɵ�P1��1+![]() ��2����P2��1-
��2����P2��1-![]() ��2����
��2����
��y=��2ʱ��x=0���ɵ�P3��0����2����
����������P��������1+ ![]() ��2����1��
��2����1��![]() ��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�
��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�


 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ſ�Ϊ12cm����ϰֽ��������������ľ����Ϊ0.6cm����Ƥ��С����ֽ�����Ͻ���ӡ��ӡ��һ�����ο�ͨͼ����ͼ���Ķ���ǡ�������������ϣ���ͼ�����������=37�㣮
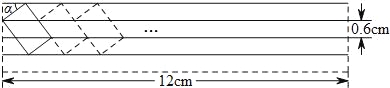
��1�������ͼ���������
��2����С���ڵ�һ��ͼ�����ұ���ͬ���ķ�ʽ������ӡ����ͼ���������ӡ����������ͼ�������ο����ݣ�sin37����0.6��cos37����0.8��tan37����0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=��2��m��x+2��ͼ��������A��x1��y1����B��x2��y2������x1��x2ʱ����y1��y2����ôm��ȡֵ��Χ��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڡ��Ƽ����´�������������һ������̨����Ʒ���ֺ���֧�ܵĴ�ϸ���õ����IJ���ṹͼ��ͼ��ʾ����̨֪�Ƶײ�֧��CDƽ����ˮƽ�棬FE��OE��GF��EF��̨���ϲ����Ƶ�O��ת��OE=20cm��EF=20![]() cm��
cm��
��1����ͼ1������̨���ϲ��Ƶ�O��ʱ��ת��������G����ֱ��CD��ʱ����������EOG=65�㣬��FG�ij��ȣ������ȷ��0.1cm����
��2����̨����ͼ1λ����ת��ͼ2��λ�ã�����ʱF��O�������ڵ�ֱ��ǡ����CD��ֱ�����F����ת���������γɵĻ��ij��ȣ����ο����ݣ�sin65����0.91��cos65����0.42��tan65����2.14��![]() ��1.73����ʹ�ÿ�ѧ��������
��1.73����ʹ�ÿ�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x=3�ǹ���x�ķ���x+m=2x��1�Ľ⣬��(m+1)2��ֵ�ǣ� ��
A.1
B.9
C.0
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ� ��
A.a2+a3=a5
B.a3a4=a12
C.a6��a3=a2
D.4a��a=3a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���A������Ϊ��2��0������COA=60����������OABC������ԭ��O��ʱ����ת120���õ�����ODEF�����߶�OB= ��ͼ����Ӱ���ֵ����Ϊ ��
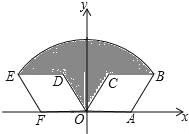
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com