
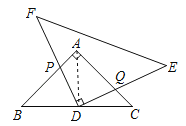
����Ŀ��������ֱ��������ABC��AB��AC����BAC��90�����͵���ֱ��������DEF��DE��DF����EDF��90������ͼ1�ڷţ���D��BC�ߵ��е��ϣ���A��DE�ϣ�

��1����գ�AB��EF��λ�ù�ϵ���� ����
��2����DEF�Ƶ�D��˳ʱ�뷽��ת����ͼ2��ʾλ��ʱ��DF��DE�ֱ�AB��AC�ڵ�P��Q����֤����BPD+��DQC��180����
��3����ͼ2������DEF�Ƶ�D��˳ʱ�뷽��ת�������У�ʼ�յ�P������A�㣬��ABC�������ΪS1���ı���APDQ�������ΪS2����ôS1��S2֮���Ƿ���ڲ����������ϵ�������ڣ���д������֮���������ϵ��֤�����������ڣ���˵�����ɣ�
���𰸡���1��ƽ�У���2������������3�����ڣ�S1��2S2�����ɼ�����.
��������
��1�����ݵ���ֱ�������ε����ʺ�ƽ���ߵ��ж��������ɵõ����ۣ�
��2�����ݵ���ֱ�������ε����ʵõ���B����C��45�㣬�ٸ��������ε��ڽǺͼ��ɵõ����ۣ�
��3������AD�����ݵ���ֱ�������ε����ʺ���ǵ����ʿɵ�BD��CD��AD����B����CAD����BDP����ADQ�������ɸ���ASA֤����BDP�ա�ADQ���ٸ���ȫ�������ε����ʼ��ɵõ����ۣ�
�⣺��1����AB��AC����BAC��90�������ABD����C=45����
��DE��DF����EDF��90�������F����E��45����
���F���� ABD����AB��EF��
�ʴ�Ϊ��ƽ�У�
��2����AB��AC����BAC��90�㣬���B����C��45�㣬
�ߡ�EDF��90�㣬���BDP+��CDQ��90�㣬
���BPD+��DQC��360�㩁��B����C����BDP����CDQ��180�㣻
��3��S1��S2֮����ڲ����������ϵ��S1��2S2.
���ɣ�����AD����ͼ����AB��AC��AD��BC��
��BD��CD��AD��![]() BC����B����C����CAD��45����
BC����B����C����CAD��45����
�ߡ�BDP+��ADP����ADP+��ADQ��90����
���BDP����ADQ��
���BDP�ա�ADQ��ASA����
��S��ABD��S��BPD+S��APD��S��ADQ+S��APD��S2��
�֡�S��ADB��![]() S1��
S1��
��S1��2S2��


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ����
����![]() ��
��![]() ��
��![]() ���㣮
���㣮
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ��ͼ�����������ߵĶԳ������Ƿ���ڵ�
��ͼ�����������ߵĶԳ������Ƿ���ڵ�![]() ��ʹ���ı���
��ʹ���ı���![]() ���ܳ���С�������ڣ�����ı���
���ܳ���С�������ڣ�����ı���![]() �ܳ�����Сֵ���������ڣ���˵�����ɣ�
�ܳ�����Сֵ���������ڣ���˵�����ɣ�
![]() ��ͼ������
��ͼ������![]() ���߶�
���߶�![]() ��һ���㣬����
��һ���㣬����![]() �����߶�
�����߶�![]() ���Ƿ���������ĵ�
���Ƿ���������ĵ�![]() ��ʹ
��ʹ![]() Ϊ������������
Ϊ������������![]() Ϊֱ�������Σ������ڣ����
Ϊֱ�������Σ������ڣ����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC�������������ֱ�ΪA����5��1����B����4��4����C����1����1����
��1����ͼ1�л�����ABC����y��ԳƵ�ͼ�Ρ�A1B1C1��
��2��ֱ��д����A1B1C1�������
��3����ͼ2��y�����ҳ���P��ʹPB+PC��ֵ��С��������ͼ�ۼ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() ���㣮
���㣮
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ��
��![]() �Ϸ�������������һ����
�Ϸ�������������һ����![]() ��
��
����ͼ![]() ������
������![]() �˶���ijλ��ʱ����
�˶���ijλ��ʱ����![]() ��
��![]() Ϊ�ڱߵ�ƽ���ı��ε��ĸ�����ǡ��Ҳ���������ϣ������ʱ��
Ϊ�ڱߵ�ƽ���ı��ε��ĸ�����ǡ��Ҳ���������ϣ������ʱ��![]() �����ꣻ
�����ꣻ
����ͼ![]() ������
������![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��F�ֱ��DZ�AD��BC���е㣬AC�ֱ�BE��DF��C��H�����ж����н��ۣ���1��BE=DF����2��AG=GH=HC����3��EG=![]() BG����4��S��ABE=3S��AGE��������ȷ�Ľ����У�������
BG����4��S��ABE=3S��AGE��������ȷ�Ľ����У�������
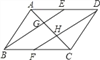
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�CD�DZ�AB�ϵĸߣ���![]() ��
��

��1����֤����ACD�ס�CBD��
��2������ACB�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() �ı���
�ı���![]() �����ǵ������Ϊ
�����ǵ������Ϊ![]() �����ǵĶ�Ӧ�Խ��ߵı�Ϊ________�������ǵ��ܳ�֮��Ϊ
�����ǵĶ�Ӧ�Խ��ߵı�Ϊ________�������ǵ��ܳ�֮��Ϊ![]() �����ı���
�����ı���![]() ���ܳ�Ϊ________��
���ܳ�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���MNPQ�У�����R�ӵ�N����������N-P-Q-M�����ƶ���Mֹͣ����R�ƶ�·��Ϊx��MNR���Ϊy����ôy��x�Ĺ�ϵ��ͼ�ڣ�����˵������ȷ���ǣ� ��

A.��x=2ʱ��y=5B.����MNPQ�ܳ���18
C.��x=6ʱ��y=10D.��y=8ʱ��x=10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() .������һ���ǣ�ʹ������
.������һ���ǣ�ʹ������![]() .�������£���ͼ��
.�������£���ͼ��
��1��������![]()
��2����![]() ΪԲ�ģ����ⳤΪ�뾶��������
ΪԲ�ģ����ⳤΪ�뾶��������![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��3����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶����
Ϊ�뾶����![]() ����
����![]() ��
��![]() ;
;
��4����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶����������
Ϊ�뾶����������![]() ��
��![]() ��
��
��5������![]() ������
������![]() .��
.��![]() �����������Ľ�.
�����������Ľ�.
��ش𣺸���ͼ�������ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com