
【题目】一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是( )
A. 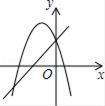 B.
B. 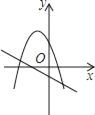 C.
C. 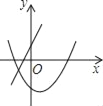 D.
D. 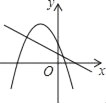
科目:初中数学 来源: 题型:
【题目】某自行车制造厂开发了一款新式自行车,计划![]() 月份生产安装
月份生产安装![]() 辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人;他们经过培训后也能独立进行安装.调研部门发现:
辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人;他们经过培训后也能独立进行安装.调研部门发现: ![]() 名熟练工和
名熟练工和![]() 名新工人每日可安装辆自行车;
名新工人每日可安装辆自行车; ![]() 名熟练工和
名熟练工和![]() 名新工人每日可安装
名新工人每日可安装![]() 辆自行车。
辆自行车。
(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘![]() 名新工人(
名新工人(![]() ).使得招聘的新工人和抽调熟练工刚好能完成
).使得招聘的新工人和抽调熟练工刚好能完成![]() 月份(
月份(![]() 天)的安装任务,那么工厂有哪几种新工人的招聘方案?
天)的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为![]() 千公里;如安装在后轮,安全行使路程为
千公里;如安装在后轮,安全行使路程为![]() 千公里.请问一对轮胎能行使的最长路程是多少千公里?
千公里.请问一对轮胎能行使的最长路程是多少千公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知正方形 ABCO,边长是 4,点 D(a,0),以 AD 为边在AD 的右侧作等腰 Rt△ADE,∠ADE=90°,连接 OE,则 OE 的最小值为__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一次函数![]() ,
,
(1)无论 k为何值,函数图像必过定点,求该点的坐标;
(2)如图 1,当 k=-![]() 时,该直线交 x 轴,y 轴于 A,B 两点,直线 l2:y=x+1 交 AB 于点 P,点 Q 是 l2 上一点,若 SABQ 6 ,求 Q 点的坐标;
时,该直线交 x 轴,y 轴于 A,B 两点,直线 l2:y=x+1 交 AB 于点 P,点 Q 是 l2 上一点,若 SABQ 6 ,求 Q 点的坐标;
(3)如图 2,在第 2 问的条件下,已知 D 点在该直线上,横坐标为 1,C 点在 x 轴负半轴, ABC=45 ,动点 M 的坐标为(a,a),求 CM+MD 的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J. Nplcr,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707-1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若![]() ,那么
,那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作:
的对数,记作:![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .
.
我们根据对数的定义可得到对数的一个性质:![]() ;理由如下:
;理由如下:
设![]() ,
,![]() ,则
,则![]() ,
,![]()
∴![]() ,由对数的定义得
,由对数的定义得![]()
又∵![]()
∴![]()
解决以下问题:
(1)将指数![]() 转化为对数式______;
转化为对数式______;
(2)证明![]()
(3)拓展运用:计算![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个四边形花坛ABCD,被两条线段MN, EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1、S2、S3、S4,若MN∥AB∥DC,EF∥DA∥CB,则有( )

A.S1= S4B.S1 + S4 = S2 + S3C.S1 + S3 = S2 + S4D.S1·S4 = S2·S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用90元钱从蔬菜批发市场批了西红柿和豆角共40kg到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.5 | 1.5 |
零售价(单位:元/kg) | 3.5 | 2.8 |
问:(1)西红柿和豆角的重量各是多少?(列二元一次方程组求解)
(2)他当天卖完这些西红柿和豆角能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点![]() 在第一象限,
在第一象限,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() ,且四边形
,且四边形![]() 的面积为48.
的面积为48.

(1)如图1,直接写出点A、B、O、C的坐标:
(2)如图2,点![]() 从
从![]() 出发以每秒1个单位的速度沿
出发以每秒1个单位的速度沿![]() 轴正半轴运动,同时点
轴正半轴运动,同时点![]() 从B出发,以每秒2个单位的速度沿射线
从B出发,以每秒2个单位的速度沿射线![]() 运动,
运动,![]() 交线段
交线段![]() 于
于![]() ,设运动的时间为
,设运动的时间为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)如图3,将线段![]() 平移,使点
平移,使点![]() 的对应点恰好落在
的对应点恰好落在![]() 轴负半轴上,点
轴负半轴上,点![]() 的对应点为
的对应点为![]() ,连
,连![]() 交
交![]() 轴交于
轴交于![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标。
的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com