
分析 (1)先将原式通分,然后变为同分母分式,然后再相减,即可解答本题;
(2)先将原式能因式分解的先因式分解,然后再化简即可解答本题.
解答 解:(1)$\frac{{a}^{2}}{a-1}$-a-1
=$\frac{{a}^{2}}{a-1}-(a+1)$
=$\frac{{a}^{2}-(a+1)(a-1)}{a-1}$
=$\frac{{a}^{2}-{a}^{2}+1}{a-1}$
=$\frac{1}{a-1}$;
(2)$\frac{{a}^{2}-4}{{a}^{2}-2a+1}$•$\frac{{a}^{2}-1}{{a}^{2}+4a+4}$
=$\frac{(a+2)(a-2)}{(a-1)^{2}}×\frac{(a+1)(a-1)}{(a+2)^{2}}$
=$\frac{(a-2)(a+1)}{(a-1)(a+2)}$
=$\frac{{a}^{2}-a-2}{{a}^{2}+a-2}$.
点评 本题考查分式的混合运算,解题的关键是明确分式的混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,以点D为圆心,DC为半径作圆弧$\widehat{CE}$,点F在边BC上,AF切$\widehat{CE}$于点E.
如图,在矩形ABCD中,以点D为圆心,DC为半径作圆弧$\widehat{CE}$,点F在边BC上,AF切$\widehat{CE}$于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果|a|>|b|,那么a2>b2 | B. | 如果a>b,那么a>-b | ||
| C. | 如果a<b,那么|a|<|b| | D. | 如果|a|=2,那么a=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
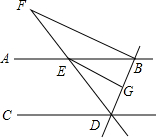 如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°.
如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | 5 | 7 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
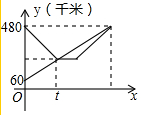 甲、乙两车分别从相距480千米的A、B两地出发,匀速相向行驶,乙车比甲车先出发1小时,从B地直达A地.甲车出发t小时两车相遇后甲车停留1小时,因有事按原路返回A地,两车同时到达A地.从甲车出发时开始计时,时间为x(时),甲、乙两车距B地的路程y(千米)与x(时)之间的函数关系如图所示
甲、乙两车分别从相距480千米的A、B两地出发,匀速相向行驶,乙车比甲车先出发1小时,从B地直达A地.甲车出发t小时两车相遇后甲车停留1小时,因有事按原路返回A地,两车同时到达A地.从甲车出发时开始计时,时间为x(时),甲、乙两车距B地的路程y(千米)与x(时)之间的函数关系如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com