
分析 求方程x2-16=0的解,可先移项,变成x2=16,从而把问题转化为求16的平方根;
求方程(x+2)2=3的解,可把x+2看作一个整体,从而把问题转化为求3的平方根.
解答 解:移项,得x2=16,
开方,得x=±4;
开方,得x+2=±$\sqrt{3}$,
解得x1=-2+$\sqrt{3}$,x2=-2-$\sqrt{3}$.
故答案为x=±4;x1=-2+$\sqrt{3}$,x2=-2-$\sqrt{3}$.
点评 本题考查了解一元二次方程-直接开平方法,注意:
(1)用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.
(2)运用整体思想,会把被开方数看成整体.
(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:单选题
下列多项式中是完全平方式的是( )
A. 2x2+4x-4 B. 16x2-8y2+1 C. 9a2-12a+4 D. x2y2+2xy+y2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
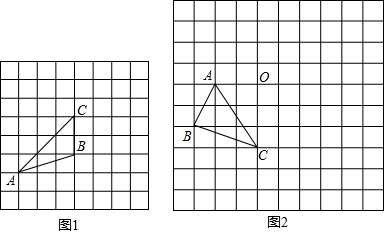
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
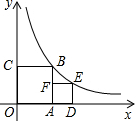 如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=$\frac{1}{x}$(x>0)的图象上,则:
如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=$\frac{1}{x}$(x>0)的图象上,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
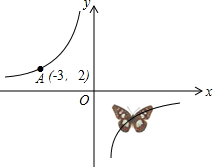 如图,反比例函数y=$\frac{k}{x}$(k≠0,k是常数)的图象经过A点,则该函数图象上被蝴蝶遮住的点的坐标可能是( )
如图,反比例函数y=$\frac{k}{x}$(k≠0,k是常数)的图象经过A点,则该函数图象上被蝴蝶遮住的点的坐标可能是( )| A. | (-2,3) | B. | (2,-2) | C. | (-1,6) | D. | (2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com