
分析 (1)由已知易得整数与分数的分子分母的关系,根据规律写出即可;
(2)根据(1)的规律易得当n=$\frac{1}{2}$时,分子为$\frac{1}{2}$,分母为$\frac{1}{2}-1$=$-\frac{1}{2}$,可得结果;当n=-2时,分子为-2,分母为-3,可得结果;
(3)由规律可得b=$\frac{a}{a-1}$,代入证明即可.
解答 (1)解:∵2+2=2×2,3+$\frac{3}{2}$=3×$\frac{3}{2}$,
∴第3个等式应该是:4+$\frac{4}{4-1}$=4$+\frac{4}{3}$=4×$\frac{4}{3}$;n个等式应该是:n+$\frac{n}{n-1}$=n×$\frac{n}{n-1}$,
故答案为:$\frac{4}{3}$=4×$\frac{4}{3}$,$\frac{n}{n-1}$=n×$\frac{n}{n-1}$;
(2)解:由(1)的规律得:
当n=$\frac{1}{2}$时,分子为$\frac{1}{2}$,分母为$\frac{1}{2}-1$=$-\frac{1}{2}$,
∴等式为:$\frac{1}{2}+$(-1)=$\frac{1}{2}$×(-1);
当n=-2时,分子为-2,分母为-3,
∴等式为:(-2)$+\frac{2}{3}$=(-2)×$\frac{2}{3}$;
故答案为:(-1)=$\frac{1}{2}×(-1)$,$\frac{2}{3}$=(-2)×$\frac{2}{3}$;
(3)证明:∵a,b是满足规律的两个数,
∴b=$\frac{a}{a-1}$,
∴$\frac{1}{b}=\frac{a-1}{a}$,
∴$\frac{1}{b}=1-\frac{1}{a}$,
∴$\frac{1}{a}+\frac{1}{b}$=1.
点评 本题主要考查了数字的变化规律,根据已知分析得出规律是解答此题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 64$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 经过不在同一直线上的三个点一定可以作圆 | |
| B. | 三角形的外心到三角形各顶点的距离相等 | |
| C. | 经过切点且垂直于切线的直线必经过圆心 | |
| D. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:单选题
如果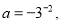
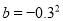 ,
, 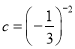 ,
, 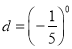 那么
那么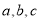 ,d三数的大小为( )
,d三数的大小为( )
A. 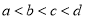 B.
B.  C.
C. 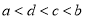 D.
D. 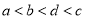
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com