
【题目】如图,抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣2,0)、B(4,0),与y轴交于点C,且OC=2OA.
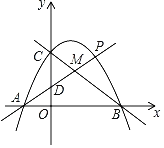
(1)该抛物线的解析式为 ;
(2)直线y=kx+l(k>0)与y轴交于点D,与直线BC交于点M,与抛物线上直线BC上方部分交于点P,设m=![]() ,求m的最大值及此时点P的坐标;
,求m的最大值及此时点P的坐标;
(3)若点D、P为(2)中求出的点,点Q为x轴的一个动点,点N为坐标平面内一点,当以点P、D、Q、N为顶点的四边形为矩形时,直接写出点N的坐标.
【答案】(1)y=﹣![]() x2+x+4;(2)当n=2时,m有最大值,最大值为
x2+x+4;(2)当n=2时,m有最大值,最大值为![]() ,此时P(2,4);(3)满足条件的点N坐标为(
,此时P(2,4);(3)满足条件的点N坐标为(![]() ,3)或(6,﹣3).
,3)或(6,﹣3).
【解析】
(1)因为抛物线y=ax2+bx+c经过A(-2,0)、B(4,0)两点,所以可以假设y=a(x+2)(x-4),求出点C坐标代入求出a即可;
(2)由△CMD∽△FMP,可得![]() ,根据m关于n的二次函数,利用二次函数的性质即可解决问题;
,根据m关于n的二次函数,利用二次函数的性质即可解决问题;
(3)存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形.分两种情形讨论:①当DP是矩形的边时,有两种情形;②当DP是对角线时,利用相似三角形的性质和勾股定理可求解.
(1)因为抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)两点,
所以可以假设y=a(x+2)(x﹣4),
∵OC=2OA,OA=2,
∴C(0,4),代入抛物线的解析式得到a=﹣![]() ,
,
∴y=﹣![]() (x+2)(x﹣4)=﹣
(x+2)(x﹣4)=﹣![]() x2+x+4,
x2+x+4,
故答案为:y=﹣![]() x2+x+4;
x2+x+4;
(2)如图1中,由题意,点P在y轴的右侧,作PE⊥x轴于E,交BC于F.
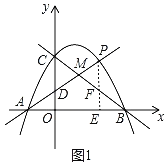
∵CD∥PE,
∴△CMD∽△FMP,
∴m=![]() ,
,
∵直线y=kx+1(k>0)与y轴交于点D,则D(0,1),
∵BC的解析式为y=﹣x+4,
设P(n,﹣![]() n2+n+4),则F(n,﹣n+4),
n2+n+4),则F(n,﹣n+4),
∴PF=﹣![]() n2+n+4﹣(﹣n+4)=﹣
n2+n+4﹣(﹣n+4)=﹣![]() (n﹣2)2+2,
(n﹣2)2+2,
∴m=![]() =﹣
=﹣![]() (n﹣2)2+
(n﹣2)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当n=2时,m有最大值,最大值为![]() ,此时P(2,4);
,此时P(2,4);
(3)存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形.
①当DP是矩形的边时,有两种情形,
a、如图2﹣1中,四边形DQNP是矩形时,
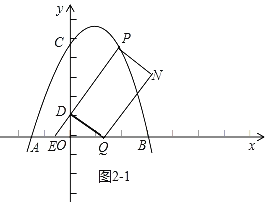
有(2)可知P(2,4),代入y=kx+1中,得到k=![]() ,
,
∴直线DP的解析式为y=![]() x+1,可得D(0,1),E(﹣
x+1,可得D(0,1),E(﹣![]() ,0),
,0),
由△DOE∽△QOD可得![]() ,
,
∴OD2=OEOQ,
∴1=![]() OQ,
OQ,
∴OQ=![]() ,
,
∴Q(![]() ,0).
,0).
根据矩形的性质,将点P向右平移![]() 个单位,向下平移1个单位得到点N,
个单位,向下平移1个单位得到点N,
∴N(2+![]() ,4﹣1),即N(
,4﹣1),即N(![]() ,3)
,3)
b、如图2﹣2中,四边形PDNQ是矩形时,
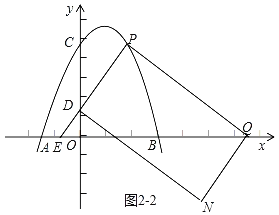
∵直线PD的解析式为y=![]() x+1,PQ⊥PD,
x+1,PQ⊥PD,
∴直线PQ的解析式为y=﹣![]() x+
x+![]() ,
,
∴Q(8,0),
根据矩形的性质可知,将点D向右平移6个单位,向下平移4个单位得到点N,
∴N(0+6,1﹣4),即N(6,﹣3).
②当DP是对角线时,设Q(x,0),则QD2=x2+1,QP2=(x﹣2)2+42,PD2=13,
∵Q是直角顶点,
∴QD2+QP2=PD2,
∴x2+1+(x﹣2)2+16=13,
整理得x2﹣2x+4=0,方程无解,此种情形不存在,
综上所述,满足条件的点N坐标为(![]() ,3)或(6,﹣3).
,3)或(6,﹣3).


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】根据某网站调查,2019年网民最关注的热点话题分别是:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据绘制的统计图如图:
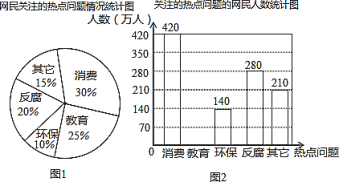
根据以上信息解答下列问题:
(1)请补全条形图,并在图中标明相应数据.
(2)若某市中心城区约有90万人口,请你估计该市中心城区最关注教育问题的人数约有多少万人?
(3)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年关注该问题网民数的年平均增长率约为多少?(已知2017~2019年每年接受调查的网民人数相同,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A1(1,1),将点A1向上平移1个单位长度,再向右平移2个单位长度得到点A2;将点A2向上平移2个单位长度,再向右平移4个单位长度得到点A3;将点A3向上平移4个单位长度,再向右平移8个单位长度得到点A4,…按这个规律平移下去得到点An(n为正整数),则点An的坐标是( )
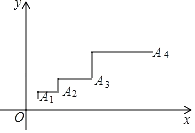
A.(2n,2n﹣1)B.(2n﹣1,2n)
C.(2n﹣1,2n+1)D.(2n﹣1,2n﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
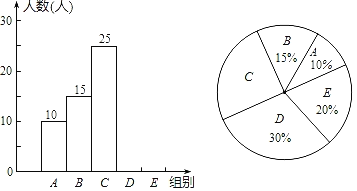
【题目】为挑选优秀同学参加云南省级英语听说能力竞赛,某中学举行了“英语单词听写”竞赛,每位学生听写单词99个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
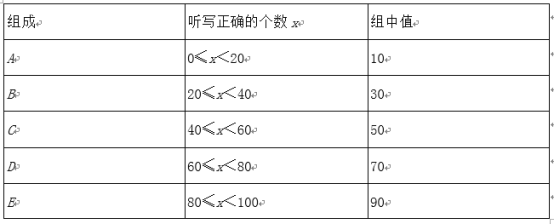
根据以上信息解决下列问题:
(1)本次共随机抽查了 名学生,并补全频数分布直方图;
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有3000名学生,如果听写正确的个数少于60个定为不合格,请你估计这所学校本次竞赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进消费,杭州市政府开展发放政府补贴消费的“消费券”活动,一超市的月销售额逐步增加.据统计,2月份销售额为200万元,4月份销售额为500万元.若3,4月平均每月的增长率为x,则( )
A.200(1+x)=500B.200(1+x)+200+(1+x)2=500
C.200(1+x)2=500D.200+200(1+x)+200(1+x)2=500
查看答案和解析>>
科目:初中数学 来源: 题型:
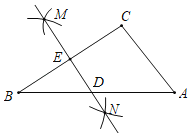
【题目】如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,大于![]() BC的长为半径作弧,两弧相交于点M和N;②作直线MN,分别交边AB,BC于点D和E,连接CD.若∠BCA=90°,AB=8,则CD的长为_____.
BC的长为半径作弧,两弧相交于点M和N;②作直线MN,分别交边AB,BC于点D和E,连接CD.若∠BCA=90°,AB=8,则CD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com