
【题目】已知:在⊙O中,直径AB=4,点P、Q均在⊙O上,且∠BAP=60°,∠BAQ=30°,则弦PQ的长为_____.
【答案】2或4
【解析】
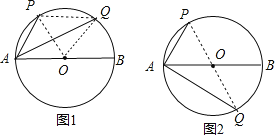
当点P和Q在AB的同侧,如图1,连接OP、OQ、PQ,先计算出∠PAQ=30°,根据圆周角定理得到∠POQ=60°,则可判断△OPQ为等边三角形,从而得到PQ=OP=2;当点P和Q在AB的同侧,如图1,连接PQ,先计算出∠PAQ=90°,根据圆周角定理得到PQ为直径,从而得到PQ=4.
解:当点P和Q在AB的同侧,如图1,连接OP、OQ、PQ,
∵∠BAP=60°,∠BAQ=30°,
∴∠PAQ=30°,
∴∠POQ=2∠PAQ=2×30°=60°,
∴△OPQ为等边三角形,
∴PQ=OP=2;
当点P和Q在AB的同侧,如图1,连接PQ,
∵∠BAP=60°,∠BAQ=30°,
∴∠PAQ=90°,
∴PQ为直径,
∴PQ=4,
综上所述,PQ的长为2或4.
故答案为2或4.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,顶点为点
,顶点为点![]() ,抛物线与
,抛物线与![]() 轴交于
轴交于![]() 、
、![]() 点(点
点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)若抛物线经过点![]() 时,求此时抛物线的解析式;
时,求此时抛物线的解析式;
(2)直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,若
两点,若![]() ,请求出
,请求出![]() 的取值范围;
的取值范围;
(3)如图,若直线![]() 交
交![]() 轴于点
轴于点![]() ,请求
,请求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一海轮位于灯塔P的西南方向,距离灯塔40了2海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店用3600元按批发价购买了一批花卉.若将批发价降低10%,则可以多购买该花卉20盆.市场调查反映,该花卉每盆售价25元时,每天可卖出25盆.若调整价格,每盆花卉每涨价1元,每天要少卖出1盆.
(1)该花卉每盆批发价是多少元?
(2)若每天所得的销售利润为200元时,且销量尽可能大,该花卉每盆售价是多少元?
(3)为了让利给顾客,该花店决定每盆花卉涨价不超过5元,问该花卉一天最大的销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,AC是⊙O的直径,AD是⊙O的切线.点E在直径AC上,连接ED交⊙O于点B,连接AB,且AB=BD.
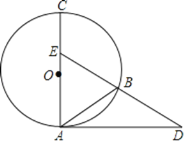
(1)求证:AB=BE;
(2)若⊙O的半径长为5,AB=6,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
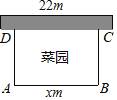
【题目】如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(矩形ABCD),墙长为22m,这个矩形的长AB=xm,菜园的面积为Sm2,且AB>AD.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围.
(2)若要围建的菜园为100m2时,求该莱园的长.
(3)当该菜园的长为多少m时,菜园的面积最大?最大面积是多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
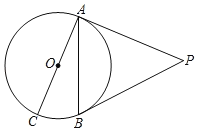
【题目】如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径.
(1)若∠BAC=25°,求∠P的度数;
(2)若∠P=60°,PA=2![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
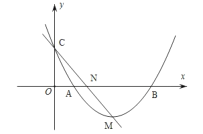
【题目】如图,抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣2,0)、B(4,0),与y轴交于点C,且OC=2OA.
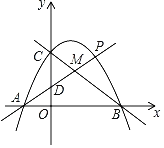
(1)该抛物线的解析式为 ;
(2)直线y=kx+l(k>0)与y轴交于点D,与直线BC交于点M,与抛物线上直线BC上方部分交于点P,设m=![]() ,求m的最大值及此时点P的坐标;
,求m的最大值及此时点P的坐标;
(3)若点D、P为(2)中求出的点,点Q为x轴的一个动点,点N为坐标平面内一点,当以点P、D、Q、N为顶点的四边形为矩形时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,①△BCE是等边三角形,②DE=BF,③△ABC≌△CFD,④四边形BEDF是平行四边形.则其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com