
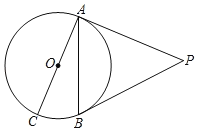
【题目】如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径.
(1)若∠BAC=25°,求∠P的度数;
(2)若∠P=60°,PA=2![]() ,求AC的长.
,求AC的长.
【答案】(1)50°;(2)4.
【解析】
(1)利用切线的性质求出∠PAB=90°﹣∠BAC=90°﹣25°=65°,根据切线长定理得到∠PBA=∠PAB=65°,再根据三角形的内角和定理求出∠P的度数;
(2)连接BC,证明△PAB是等边三角形,求出![]() ,∠PAB=60°,由AC是⊙O的直径得到∠ABC=90°,利用AC=
,∠PAB=60°,由AC是⊙O的直径得到∠ABC=90°,利用AC=![]() 求出答案.
求出答案.
(1)∵PA为切线,
∴OA⊥PA,
∴∠CAP=90°,
∴∠PAB=90°﹣∠BAC=90°﹣25°=65°.
∵PA,PB是⊙O的切线,
∴PA=PB,
∴∠PBA=∠PAB=65°,
∴∠P=180°﹣65°﹣65°=50°;
(2)连接BC.
∵PA,PB是⊙O的切线,
∴PA=PB,∠CAP=90°.
∵∠P=60°,
∴△PAB是等边三角形,
∴![]() ,∠PAB=60°,
,∠PAB=60°,
∴∠CAB=30°.
∵AC是⊙O的直径,
∴∠ABC=90°,
∴AC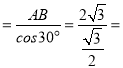 4.
4.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
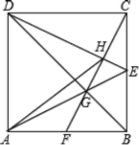
【题目】如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①CF⊥DE;②![]() ;③AD=AH;④GH=
;③AD=AH;④GH=![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
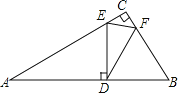
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与两坐标轴分别交于点A、B、C,直线y=﹣![]() x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
(1)求抛物线的解析式.
(2)已知点N在对称轴上,且AN+DN的值最小.求点N的坐标.
(3)在(2)的条件下,若点E与点C关于对称轴对称,请你画出△EMN并求它的面积.
(4)在(2)的条件下,在坐标平面内是否存在点P,使以A、B、N、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
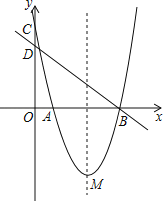
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A1(1,1),将点A1向上平移1个单位长度,再向右平移2个单位长度得到点A2;将点A2向上平移2个单位长度,再向右平移4个单位长度得到点A3;将点A3向上平移4个单位长度,再向右平移8个单位长度得到点A4,…按这个规律平移下去得到点An(n为正整数),则点An的坐标是( )
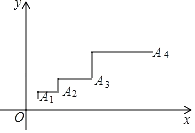
A.(2n,2n﹣1)B.(2n﹣1,2n)
C.(2n﹣1,2n+1)D.(2n﹣1,2n﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
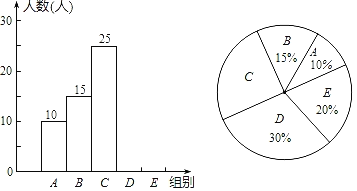
【题目】为挑选优秀同学参加云南省级英语听说能力竞赛,某中学举行了“英语单词听写”竞赛,每位学生听写单词99个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
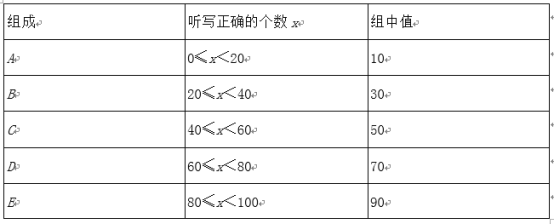
根据以上信息解决下列问题:
(1)本次共随机抽查了 名学生,并补全频数分布直方图;
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有3000名学生,如果听写正确的个数少于60个定为不合格,请你估计这所学校本次竞赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,G、A、B在同一直线上,点E在AD上,连接DG,BE.
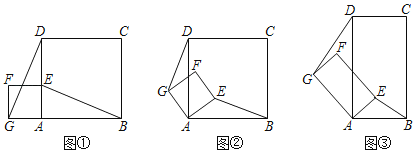
(1)证明:BE=DG;
(2)发现:当正方形AEFG绕点A旋转,如图②所示,判断BE与DG的数量关系和位置关系,并说明理由;
(3)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,判断BE与DG的数量关系和位置关系是否与(2)的结论相同,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com