
����Ŀ����ͼ����ʾ����֪������ABCD��������AEFG��G��A��B��ͬһֱ���ϣ���E��AD�ϣ�����DG��BE��
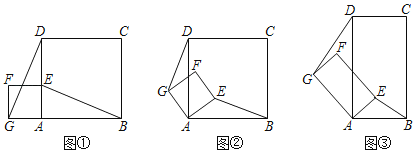
��1��֤����BE��DG��
��2�����֣���������AEFG�Ƶ�A��ת����ͼ����ʾ���ж�BE��DG��������ϵ��λ�ù�ϵ����˵�����ɣ�
��3��̽������ͼ����ʾ�����ı���ABCD���ı���AEFG��Ϊ���Σ���AD��2AB��AG��2AEʱ���ж�BE��DG��������ϵ��λ�ù�ϵ�Ƿ��루2���Ľ�����ͬ����˵�����ɣ�
���𰸡���1��֤������������2��BE��DG��BE��DG�����ɼ���������3��������ϵ��������BE��DG��DG��2BE�����ɼ�������λ�ù�ϵ���������ɼ�����
��������
��1�����������ε����ʼ�ȫ�������ε��ж��ɵ���ABE�ա�DAG��SAS�����ٸ���ȫ�������ε����ʼ��ɵó����ۣ�
��2�����������ε����ʿ�֪��AE��AG��AB��AD����BAD����EAG��90�����ٸ���ͬ�ŵ������ȵó���BAE����DAG��Ȼ�����ȫ�������ε��ж������ó���ABE�ա�DAG��SAS������ȫ�������ε����ʶ����ɵó�BE��DG����ABE����ADG���ӳ�BE��AD��T����DG��H�������ó���DHB=90�㣬��BE��DG��
��3�������ı���ABCD���ı���AEFG���Ǿ��Σ���AD��2AB��AG��2AEʱ������ABE�ס�ADG���ٸ������������ε����ʼ��ɵó����ۣ�
�⣺��1��֤�������ı���ABCD���ı���AEFG�������Σ�
��AE��AG��AB��AD����BAD����EAG��90����
���ABE�ա�DAG��SAS����
��BE��DG��
��2��BE��DG��BE��DG��
��ͼ1�У����ı���ABCD���ı���AEFG�������Σ�
��AE��AG��AB��AD����BAD����EAG��90����
���BAE����DAG��
����ABE����DAG��
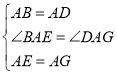 ��
��
���ABE�ա�DAG��SAS����
��BE��DG����ABE����ADG��
�ӳ�BE��AD��T����DG��H��

�ߡ�ATB+��ABE��90����
���ATB+��ADG��90����
�ߡ�ATB����DTH��
���DTH+��ADG��90����
���DHB��90����
��BE��DG��
��3��������ϵ�����������ǵ�������ϵΪDG��2BE��λ�ù�ϵ������
��ͼ2�У��ӳ�BE��AD��T����DG��H��
���ı���ABCD���ı���AEFG��Ϊ���Σ�
���BAD����DAG��
���BAE����DAG��
��AD��2AB��AG��2AE��
��![]() ��
��
���ABE�ס�ADG��
���ABE����ADG��![]() ��
��
��DG��2BE��
�ߡ�ATB+��ABE��90����
���ATB+��ADG��90����
�ߡ�ATB����DTH��
���DTH+��ADG��90����
���DHB��90����
��BE��DG��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
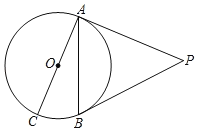
����Ŀ����ͼ��PA��PB����O�����ߣ�A��BΪ�е㣬AC����O��ֱ����
��1������BAC=25�㣬���P�Ķ�����
��2������P=60�㣬PA=2![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ�ƻ����̵깺��ͬһ��Ʒ�ƵĸֱʺͱʼDZ�����֪����һ֧�ֱʱȹ���һ���ʼDZ�����20Ԫ������1500Ԫ����ֱʺ���600Ԫ����ʼDZ�������ֱʵ������ǹ���ʼDZ�������һ�룮
��1������һ֧�ֱʡ�һ���ʼDZ�����Ҫ����Ԫ��
��2������̸���̵�����Żݣ��Żݷ�ʽ��ÿ����һ֧�ֱ�����һ���ʼDZ�������˵�λ��Ҫ�ʼDZ��������Ǹֱ�������3������6�����ҹ���ֱʺͱʼDZ����ܷ��ò�����1020Ԫ����ô���ɹ������֧�ֱʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90������ACB=30��������ABC�Ƶ�C˳ʱ����ת60���õ���DEC����A��B�Ķ�Ӧ��ֱ���D��E����F�DZ�AC�е㣬����BCE�ǵȱ������Σ���DE=BF������ABC�ա�CFD�����ı���BEDF��ƽ���ı��Σ���������ȷ���۵ĸ�����(����)

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
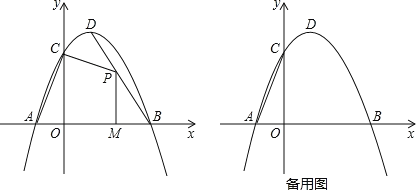
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=��ax2+bx+3��x�ύ��A(��1��0)��B(3��0)���㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣮
��1����ֱ��AC�������ߵĽ���ʽ�������D������ꣻ
��2����PΪ�߶�BD�ϵ�һ�����㣬����P��PM��x���ڵ�M�����ı���PMAC����������ֵ�ʹ�ʱ��P�����ꣻ
��3������P��x����һ�����㣬��P��ֱ��1��AC���������ڵ�Q����̽��������P����˶��������������Ƿ���ڵ�Q��ʹ�Ե�A��P��Q��CΪ������ı�����ƽ���ı��Σ������ڣ���������������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��12������������ʡ�人�в���ҽԺ½�����ֲ���ԭ����ײ���������֤ʵ�÷���Ϊһ������״������Ⱦ�ķ��ף��䴫Ⱦ�Խ�ǿ.Ϊ����Ч�ر��⽻���Ⱦ����Ҫ��ȡ���·�����ʩ���ٴ����֣�����ϴ�֣����ٳ��ţ����ظ��룻����ڱǣ������ԣ�ij��˾Ϊ�˽�Ա���Է�����ʩ���˽�̶ȣ��������˽⡢�˽���١������˽�ͺ��˽⣩��ͨ�������ʾ�����ķ�ʽ����������������飨ÿ��Ա��������ֻ��ѡ��һ����������������Ƴ���������ͳ��ͼ��
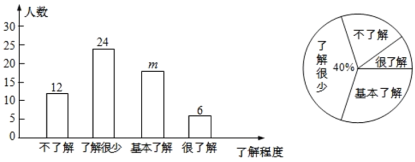
��������������Ϣ�������������
��1�����ι�������_______��Ա��������ͳ��ͼ��![]() ________��
________��
��2�����ù�˾����Ա��1000����������Ʋ��˽������ʩ��������
��3���ڵ����У�������4��Ա���Է�����ʩ���˽⣬������3����Ա����1��ŮԱ��.�����������������ȡ2���������ڹ�˾Ⱥ���ռ�������ʩ����ǡ�ó���һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOB=90�㣬��OAB=30�㣬����������![]() ��ͼ�����
��ͼ�����![]() ������������
������������![]() ��ͼ�����A
��ͼ�����A
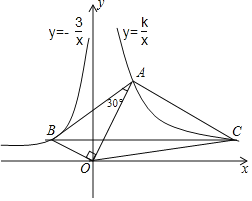
��1����![]() ��
��![]() ��ֵ.
��ֵ.
��2������B��BC��x�ᣬ��˫����![]() ���ڵ�C�����OAC�����.
���ڵ�C�����OAC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
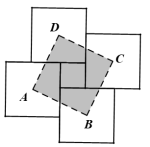
����Ŀ�����Ŀ�������ε�ש��һ��С�����ε�שƴ����ͼ��ʾ��ʵ��ͼ����ÿ��������ε�ש���Ϊa��С�����ε�ש���Ϊ���������Ŀ�������ε�ש�����ĵõ�������ABCD����������ABCD�����Ϊ____________���ú�a��b�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y1��ͼ���뷴��������y2��ͼ���ཻ�ڵ�A(2��-4)������˵����ȷ���ǣ� ��
A.����������y2�Ľ���ʽ��![]()
B.��������ͼ�����һ��������Ϊ(2��4)
C.��x��-2��0��x��2ʱ��y1��y2
D.����������y1�뷴��������y2����x���������С
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com