
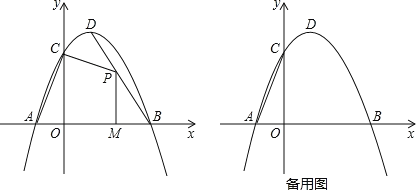
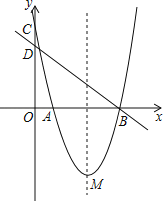
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=Љax2+bx+3гыxжсНЛгкA(Љ1ЃЌ0)ЃЌB(3ЃЌ0)СНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧИУХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓжБЯпACМАХзЮяЯпЕФНтЮіЪНЃЌВЂЧѓГіDЕуЕФзјБъЃЛ
ЃЈ2ЃЉШєPЮЊЯпЖЮBDЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPMЁЭxжсгкЕуMЃЌЧѓЫФБпаЮPMACЕФУцЛ§ЕФзюДѓжЕКЭДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуPЪЧxжсЩЯвЛИіЖЏЕуЃЌЙ§PзїжБЯп1ЁЮACНЛХзЮяЯпгкЕуQЃЌЪдЬНОПЃКЫцзХPЕуЕФдЫЖЏЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуQЃЌЪЙвдЕуAЁЂPЁЂQЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЗћКЯЬѕМўЕФЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=3x+3ЃЌy=Љx2+2x+3ЃЌЖЅЕуDЕФзјБъЮЊ(1ЃЌ4)ЃЛЃЈ2ЃЉЫФБпаЮPMACЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌДЫЪБЕуPЕФзјБъЮЊ(
ЃЌДЫЪБЕуPЕФзјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЛЃЈ3ЃЉЕуQЕФзјБъЮЊ(2ЃЌ3)Лђ(1
)ЃЛЃЈ3ЃЉЕуQЕФзјБъЮЊ(2ЃЌ3)Лђ(1![]() ЃЌЉ3)Лђ(1
ЃЌЉ3)Лђ(1![]() ЃЌЉ3)ЃЎ
ЃЌЉ3)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕуCзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпACМАХзЮяЯпЕФНтЮіЪНЃЌАбХзЮяЯпЕФвЛАуЪНзЊЛЏЮЊЖЅЕуЪНМДПЩЧѓГіDЕуЕФзјБъЃЛ
ЃЈ2ЃЉЯШИљОнД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпBDЕФНтЮіЪНЃЌЩшЕуPЕФКсзјБъЮЊpЃЌШЛКѓИљОнSЫФБпаЮPMAC=SЁїOAC+SЬнаЮOMPCМДПЩЕУГіSЫФБпаЮPMACгыpЕФЙиЯЕЪНЃЌдйИљОнЖўДЮКЏЪ§ЕФаджЪНтД№МДПЩЃЛ
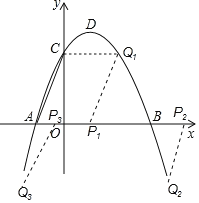
ЃЈ3ЃЉгЩЬтвтЕУPQЁЮACЧвPQ=ACЃЌЩшЕуPЕФзјБъЮЊ(xЃЌ0)ЃЌЕБЕуQдкxжсЩЯЗНЪБЃЌдђЕуQЕФзјБъЮЊ(x+1ЃЌ3)ЃЌАбЕуQЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНМДПЩЧѓГіxЃЌНјЖјПЩЕУЕуQзјБъЃЛЕБЕуQдкxжсЯТЗНЪБЃЌдђЕуQЕФзјБъЮЊ(xЉ1ЃЌЉ3)ЃЌЭЌбљЕФЗНЗЈЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЁпХзЮяЯпy=Љax2+bx+3гыyжсНЛгкЕуCЃЌ
ЁрЕуC(0ЃЌ3)ЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=k1x+b1(k1Ёй0)ЃЎ
ЁпЕуA(Љ1ЃЌ0)ЃЌЕуC(0ЃЌ3)ЃЌ
Ёр ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=3x+3ЃЎ
ЁпХзЮяЯпy=Љax2+bx+3гыxжсНЛгкA(Љ1ЃЌ0)ЃЌB(3ЃЌ0)СНЕуЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2+2x+3ЃЎ
Ёпy=Љx2+2x+3=Љ(xЉ1)2+4ЃЌ
ЁрЖЅЕуDЕФзјБъЮЊ(1ЃЌ4)ЃЛ
ЃЈ2ЃЉЩшжБЯпBDЕФНтЮіЪНЮЊy=kx+bЃЎ
ЁпЕуB(3ЃЌ0)ЃЌЕуD(1ЃЌ4)ЃЌ
Ёр![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBDЕФНтЮіЪНЮЊy=Љ2x+6ЃЎ
ЁпPЮЊЯпЖЮBDЩЯЕФвЛИіЖЏЕуЃЌ
ЁрЩшЕуPЕФзјБъЮЊ(pЃЌЉ2p+6)ЃЎ
ЁпOA=1ЃЌOC=3ЃЌOM=pЃЌPM=Љ2p+6ЃЌ
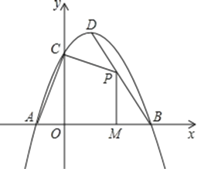
ЁрSЫФБпаЮPMAC=SЁїOAC+SЬнаЮOMPC![]() =Љp2
=Љp2![]() p
p![]() =Љ(p
=Љ(p![]() )2
)2![]() ЃЌ
ЃЌ
Ёп1ЃМpЃМ3ЃЌ
ЁрЕБp![]() ЪБЃЌЫФБпаЮPMACЕФУцЛ§ШЁЕУзюДѓжЕЮЊ
ЪБЃЌЫФБпаЮPMACЕФУцЛ§ШЁЕУзюДѓжЕЮЊ![]() ЃЌДЫЪБЕуPЕФзјБъЮЊ(
ЃЌДЫЪБЕуPЕФзјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
ЃЈ3ЃЉЁпжБЯпlЁЮACЃЌвдЕуAЁЂPЁЂQЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌ
ЁрPQЁЮACЧвPQ=ACЃЎ
ЩшЕуPЕФзјБъЮЊ(xЃЌ0)ЃЌгЩA(Љ1ЃЌ0)ЃЌC(0ЃЌ3)ЃЌ
ЕБЕуQдкxжсЩЯЗНЪБЃЌдђЕуQЕФзјБъЮЊ(x+1ЃЌ3)ЃЌ
ДЫЪБЃЌЉ(x+1)2+2(x+1)+3=3ЃЌ
НтЕУЃКx1=Љ1(ЩсШЅ)ЃЌx2=1ЃЌ
ЁрЕуQЕФзјБъЮЊ(2ЃЌ3)ЃЛ
ЕБЕуQдкxжсЯТЗНЪБЃЌдђЕуQЕФзјБъЮЊ(xЉ1ЃЌЉ3)ЃЌ
ДЫЪБЃЌЉ(xЉ1)2+2(xЉ1)+3=Љ3ЃЌ
ећРэЕУЃКx2Љ4xЉ3=0ЃЌ
НтЕУЃКx1=2![]() ЃЌx2=2
ЃЌx2=2![]() ЃЌ
ЃЌ
ЁрЕуQЕФзјБъЮЊ(1![]() ЃЌЉ3)Лђ(1
ЃЌЉ3)Лђ(1![]() ЃЌЉ3)ЃЌ
ЃЌЉ3)ЃЌ
злЩЯЫљЪіЃКЕуQЕФзјБъЮЊ(2ЃЌ3)Лђ(1![]() ЃЌЉ3)Лђ(1
ЃЌЉ3)Лђ(1![]() ЃЌЉ3)ЃЎ
ЃЌЉ3)ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bx+cгыСНзјБъжсЗжБ№НЛгкЕуAЁЂBЁЂCЃЌжБЯпyЃНЉ![]() x+4ОЙ§ЕуBЃЌгыyжсНЛЕуЮЊDЃЌMЃЈ3ЃЌЉ4ЃЉЪЧХзЮяЯпЕФЖЅЕуЃЎ
x+4ОЙ§ЕуBЃЌгыyжсНЛЕуЮЊDЃЌMЃЈ3ЃЌЉ4ЃЉЪЧХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉвбжЊЕуNдкЖдГЦжсЩЯЃЌЧвAN+DNЕФжЕзюаЁЃЎЧѓЕуNЕФзјБъЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЕуEгыЕуCЙигкЖдГЦжсЖдГЦЃЌЧыФуЛГіЁїEMNВЂЧѓЫќЕФУцЛ§ЃЎ
ЃЈ4ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌдкзјБъЦНУцФкЪЧЗёДцдкЕуPЃЌЪЙвдAЁЂBЁЂNЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЕуDдкABЩЯЃЌвдADЮЊжБОЖЕФЁбOгыБпBCЯрЧагкЕуEЃЌгыБпACЯрНЛгкЕуGЃЌЧв![]() ЃН
ЃН![]() ЃЌСЌНгGOВЂбгГЄНЛЁбOгкЕуFЃЌСЌНгBF
ЃЌСЌНгGOВЂбгГЄНЛЁбOгкЕуFЃЌСЌНгBF
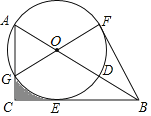
ЃЈ1ЃЉЧѓжЄЃКЂйAOЃНAGЃЌЂкBFЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉШєBDЃН6ЃЌЧѓЭМаЮжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшвЛДЮКЏЪ§y1=x+a+bКЭЖўДЮКЏЪ§y2=x(x+a)+bЃЎ
(1)Шєy1ЃЌy2ЕФЭМЯѓЖМОЙ§Еу(-2ЃЌ1)ЃЌЧѓетСНИіКЏЪ§ЕФБэДяЪНЃЛ
(2)ЧѓжЄЃКy1ЃЌy2ЕФЭМЯѓБигаНЛЕуЃЛ
(3)ШєaЃО0ЃЌy1ЃЌy2ЕФЭМЯѓНЛгкЕу(x1ЃЌm)ЃЌ(x2ЃЌn)(x1ЃМx2)ЃЌЩш(x3ЃЌn)ЮЊy2ЭМЯѓЩЯвЛЕу(x3Ёйx2)ЃЌЧѓx3-x1ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
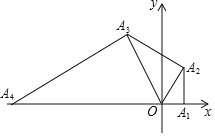
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуA1ЕФзјБъЮЊ(1ЃЌ0)ЃЌвдOA1ЮЊжБНЧБпзїRtЁїOA1A2ЃЌВЂЪЙЁЯA1OA2=60ЁуЃЌдйвдOA2ЮЊжБНЧБпзїRtЁїOA2A3ЃЌВЂЪЙЁЯA2OA3=60ЁуЃЌдйвдOA3ЮЊжБНЧБпзїRtЁїOA3A4ЃЌВЂЪЙЁЯA3OA4=60ЁуЁАДДЫЙцТЩНјааЯТШЅЃЌдђЕуA2020ЕФзјБъЮЊ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЫљЪОЃЌвбжЊе§ЗНаЮABCDКЭе§ЗНаЮAEFGЃЌGЁЂAЁЂBдкЭЌвЛжБЯпЩЯЃЌЕуEдкADЩЯЃЌСЌНгDGЃЌBEЃЎ
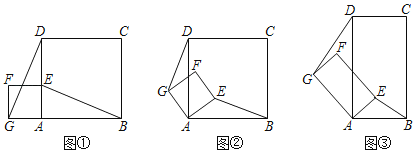
ЃЈ1ЃЉжЄУїЃКBEЃНDGЃЛ
ЃЈ2ЃЉЗЂЯжЃКЕБе§ЗНаЮAEFGШЦЕуAа§зЊЃЌШчЭМЂкЫљЪОЃЌХаЖЯBEгыDGЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЬНОПЃКШчЭМЂлЫљЪОЃЌШєЫФБпаЮABCDгыЫФБпаЮAEFGЖМЮЊОиаЮЃЌЧвADЃН2ABЃЌAGЃН2AEЪБЃЌХаЖЯBEгыDGЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЪЧЗёгыЃЈ2ЃЉЕФНсТлЯрЭЌЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫАяжњБОЪавЛУћЛМЁААзбЊВЁЁБЕФИпжаЩњЃЌФГАр15УћЭЌбЇЛ§МЋОшПюЃЌЫћУЧОшПюЪ§ЖюШчЯТБэЃК
ОшПюЕФЪ§ЖюЃЈЕЅЮЛЃКдЊЃЉ | 5 | 10 | 20 | 50 | 100 |
ШЫЪ§ЃЈЕЅЮЛЃКИіЃЉ | 2 | 4 | 5 | 3 | 1 |
Йигкет15УћЭЌбЇЫљОшПюЕФЪ§ЖюЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧ
A.жкЪ§ЪЧ100 B.ЦНОљЪ§ЪЧ30 C.МЋВюЪЧ20 D.жаЮЛЪ§ЪЧ20
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌФГГЌЪаДгЕзТЅЕНЖўТЅгавЛздЖЏЗіЬнЃЌЭМ2ЪЧВрУцЪОвтЭМЃЎвбжЊздЖЏЗіЬнABЕФГЄЖШЪЧ12ЃЎ5УзЃЌMNЪЧЖўТЅТЅЖЅЃЌMNЁЮPQЃЌCЪЧMNЩЯДІдкздЖЏЗіЬнЖЅЖЫBЕуе§ЩЯЗНЕФвЛЕуЃЌBCЁЭMNЃЌдкздЖЏЗіЬнЕзЖЫAДІВтЕУCЕуЕФбіНЧЁЯCAQЮЊ45ЁуЃЌЦТНЧЁЯBAQЮЊ37ЁуЃЌЧѓЖўТЅЕФВуИпBCЃЈОЋШЗЕН0ЃЎ1УзЃЉЃЎЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0ЃЎ60ЃЌcos37ЁуЁж0ЃЎ80ЃЌtan37ЁуЁж0ЃЎ75 ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХШЫУёЩњЛюЫЎЦНЕФЬсИпКЭЛЗОГЕФВЛЖЯИФЩЦЃЌДјЖЏСЫТУгЮвЕЕФЗЂеЙЃЎФГЪаТУгЮОАЧјгаAЃЌBЃЌCЃЌDЫФИіжјУћОАЕуЃЌИУЪаТУгЮВПУХЭГМЦЛцжЦГі2019ФъгЮПЭШЅИїОАЕуЧщПіЭГМЦЭМЃЌИљОнИјГіЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
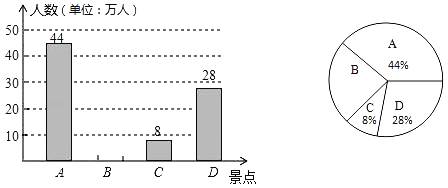
ЃЈ1ЃЉ2019ФъИУЪаТУгЮОАЧјЙВНгД§гЮПЭЁЁ ЁЁЭђШЫЃЌЩШаЮЭГМЦЭМжаCОАЕуЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЪЧЁЁ ЁЁЖШЃЛ
ЃЈ2ЃЉАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉМзЃЌввСНЮЛЭЌбЇШЅИУОАЧјТУгЮЃЌгУЪїзДЭМЛђСаБэЗЈЃЌЧѓМзЃЌввСНЮЛЭЌбЇдкAЃЌBЃЌDШ§ИіОАЕужаЃЌЭЌЪБбЁдёШЅЭЌвЛОАЕуЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com