
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,①△BCE是等边三角形,②DE=BF,③△ABC≌△CFD,④四边形BEDF是平行四边形.则其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
由直角三角形的性质和旋转的性质可得![]() ,
,![]() ,
,![]() ,
,![]() ,可判断①②;由“
,可判断①②;由“![]() ”可证
”可证![]() ,可判断③,延长
,可判断③,延长![]() 交
交![]() 于点
于点![]() ,可证
,可证![]() ,由一组对边平行且相等可证四边形
,由一组对边平行且相等可证四边形![]() 是平行四边形,即可判断④,即可求解.
是平行四边形,即可判断④,即可求解.
∵点F是边AC中点,∴CF=BF=AF![]() AC.
AC.
∵∠BCA=30°,∴BA![]() AC,∴BF=AB=AF=CF,∴∠FCB=∠FBC=30°.
AC,∴BF=AB=AF=CF,∴∠FCB=∠FBC=30°.
∵将△ABC绕点C顺时针旋转60°得到△DEC,∴∠BCE=∠ACD=60°,CB=CE,∠DEC=∠ABC=90°,AB=DE,∴△BCE是等边三角形,DE=BF,故①②正确;
∵CD=AC,AB=CF,∴Rt△ABC≌Rt△CFD(HL),故③正确;
延长BF交CE于点G,则∠BGE=∠GBC+∠BCG=90°,
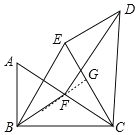
∴∠BGE=∠DEC,∴BF∥ED,∴四边形BEDF是平行四边形,故④正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】为挑选优秀同学参加云南省级英语听说能力竞赛,某中学举行了“英语单词听写”竞赛,每位学生听写单词99个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
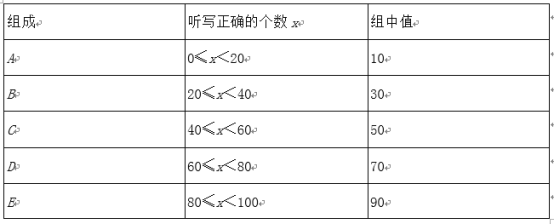
根据以上信息解决下列问题:
(1)本次共随机抽查了 名学生,并补全频数分布直方图;
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有3000名学生,如果听写正确的个数少于60个定为不合格,请你估计这所学校本次竞赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进消费,杭州市政府开展发放政府补贴消费的“消费券”活动,一超市的月销售额逐步增加.据统计,2月份销售额为200万元,4月份销售额为500万元.若3,4月平均每月的增长率为x,则( )
A.200(1+x)=500B.200(1+x)+200+(1+x)2=500
C.200(1+x)2=500D.200+200(1+x)+200(1+x)2=500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设一次函数y1=x+a+b和二次函数y2=x(x+a)+b.
(1)若y1,y2的图象都经过点(-2,1),求这两个函数的表达式;
(2)求证:y1,y2的图象必有交点;
(3)若a>0,y1,y2的图象交于点(x1,m),(x2,n)(x1<x2),设(x3,n)为y2图象上一点(x3≠x2),求x3-x1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
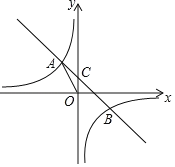
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y![]() (k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,5),点B的坐标为(5,n),tan∠AOC
(k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,5),点B的坐标为(5,n),tan∠AOC![]() .
.
(1)求k的值;
(2)直接写出点B的坐标,并求直线AB的解析式;
(3)P是y轴上一点,且S△PBC=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,G、A、B在同一直线上,点E在AD上,连接DG,BE.
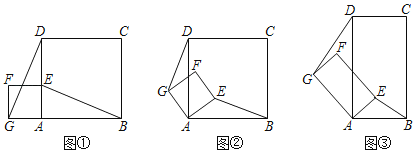
(1)证明:BE=DG;
(2)发现:当正方形AEFG绕点A旋转,如图②所示,判断BE与DG的数量关系和位置关系,并说明理由;
(3)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,判断BE与DG的数量关系和位置关系是否与(2)的结论相同,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,大于![]() BC的长为半径作弧,两弧相交于点M和N;②作直线MN,分别交边AB,BC于点D和E,连接CD.若∠BCA=90°,AB=8,则CD的长为_____.
BC的长为半径作弧,两弧相交于点M和N;②作直线MN,分别交边AB,BC于点D和E,连接CD.若∠BCA=90°,AB=8,则CD的长为_____.
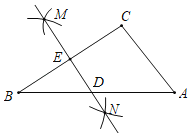
查看答案和解析>>
科目:初中数学 来源: 题型:
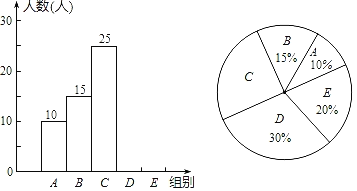
【题目】为了弘扬中国传统文化,某校对全校学生进行了古诗词知识测试,将测试成绩分为一般、良好、优秀三个等级.从中随机抽取部分学生的测试成绩,绘制成如下两幅统计图,根据图中的信息,解答下列问题:
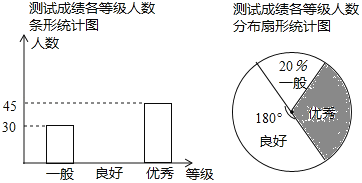
(1)本次抽样调查的样本容量是 ,扇形统计图中阴影部分扇形的圆心角是 度;
(2)将条形统计图补充完整;
(3)根据本次抽样调查的结果,试估计该校2000名学生中测试成绩为良好和优秀的共有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com