
����Ŀ��Ϊ�˺����й���ͳ�Ļ���ijУ��ȫУѧ�������˹�ʫ��֪ʶ���ԣ������Գɼ���Ϊһ�㡢���á����������ȼ������������ȡ����ѧ���IJ��Գɼ������Ƴ���������ͳ��ͼ������ͼ�е���Ϣ������������⣺
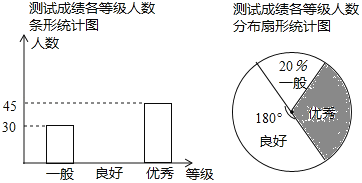
��1�����γ�������������������� ��������ͳ��ͼ����Ӱ�������ε�Բ�Ľ����� ���ȣ�
��2��������ͳ��ͼ����������
��3�����ݱ��γ�������Ľ�����Թ��Ƹ�У2000��ѧ���в��Գɼ�Ϊ���ú�����Ĺ��ж����ˣ�
���𰸡���1��150�ˣ�108����2������������3��1600��
��������
��1������һ��������������ռ�İٷֱ������������ȷ���������������������Լ��ٷֱȼ������Բ�Ľǣ�
��2��������õ��������ɻ�������ͼ��
��3��������ú�����ռ�İٷֱȣ�����2000���ɵõ������
�⣺��1����������30��20%��150���ˣ���
��Ӱ�������ε�Բ�Ľǣ�360���![]() ��108����
��108����
�ʴ�Ϊ��150�ˣ�108��
��2�����õ�������150��30��45��75���ˣ���
����ͼ��ͼ��ʾ��
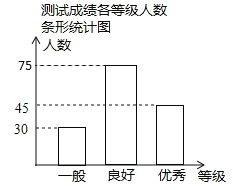
��3��У2000��ѧ���в��Գɼ�Ϊ���ú�����Ĺ��У�2000��80%��1600���ˣ�
�𣺸�У2000��ѧ���в��Գɼ�Ϊ���ú�����Ĺ���1600�ˣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90������ACB=30��������ABC�Ƶ�C˳ʱ����ת60���õ���DEC����A��B�Ķ�Ӧ��ֱ���D��E����F�DZ�AC�е㣬����BCE�ǵȱ������Σ���DE=BF������ABC�ա�CFD�����ı���BEDF��ƽ���ı��Σ���������ȷ���۵ĸ�����(����)

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ŀ�������ε�ש��һ��С�����ε�שƴ����ͼ��ʾ��ʵ��ͼ����ÿ��������ε�ש���Ϊa��С�����ε�ש���Ϊ���������Ŀ�������ε�ש�����ĵõ�������ABCD����������ABCD�����Ϊ____________���ú�a��b�Ĵ���ʽ��ʾ����
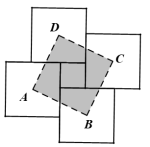
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���![]() b��c�dz�����
b��c�dz�����![]() ͼ���һ���֣���x��Ľ���A�ڵ�
ͼ���һ���֣���x��Ľ���A�ڵ�![]() ��
��![]() ֮�䣬�Գ�����
֮�䣬�Գ�����![]() ��������˵����
��������˵����![]() ��
��![]() ��
��![]() ��
��![]() Ϊʵ��������5����
Ϊʵ��������5����![]() ʱ��
ʱ��![]() ��������ȷ���ǣ� ��
��������ȷ���ǣ� ��

A.��1����2����4��B.��1����2����5��C.��2����3����4��D.��3����4����5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Ϊ120 km��ij����·AB���мס����������ֱ����վA�ͱ�վBͬʱ����������У�����B��A�����̷��ص�����վֹͣ���ٶȾ�Ϊ40 km/h����׳����ҳ�����վA��·�̷ֱ�Ϊy����y����km������ʻʱ��Ϊt��h����
��1��ͼ���ѻ���y����t�ĺ���ͼ������a��____��b��____��c��____��
��2���ֱ�д��0��t��3��3��t��6ʱ��y����ʱ��t֮��ĺ�����ϵʽ��
��3����ͼ���в���y����t֮��ĺ���ͼ���۲�ͼ��������������ʻ���������������Ĵ�����
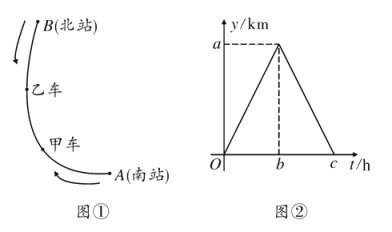
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���B�ڵ�һ���ޣ�BA��x���ڵ�A������������y��![]() ��x��0����ͼ�����߶�AB�ཻ�ڵ�C��C���߶�AB���е㣬��C����ֱ��y��x�ĶԳƵ�C'������Ϊ��m��6����m��6��������OAB�����Ϊ12����k��ֵΪ��������
��x��0����ͼ�����߶�AB�ཻ�ڵ�C��C���߶�AB���е㣬��C����ֱ��y��x�ĶԳƵ�C'������Ϊ��m��6����m��6��������OAB�����Ϊ12����k��ֵΪ��������
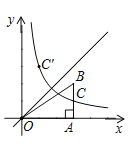
A.4B.6C.8D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y1��ͼ���뷴��������y2��ͼ���ཻ�ڵ�A(2��-4)������˵����ȷ���ǣ� ��
A.����������y2�Ľ���ʽ��![]()
B.��������ͼ�����һ��������Ϊ(2��4)
C.��x��-2��0��x��2ʱ��y1��y2
D.����������y1�뷴��������y2����x���������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�O �У�AB Ϊֱ������ P ��BA ���ӳ����ϣ�PC Ϊ��O �����ߣ����� A ��AH��PC �ڵ� H�� ����O �ڵ� D������ BC��BD��AC��
(1)��ͼ 1����֤����CAH=��CAB��
(2)��ͼ 2������ C �� CE��AB �ڵ� E����֤��BD=2CE��
(3)��ͼ 3����(2)�������£��� F ��BC �ϣ����� DF��EF���� BG=2AE����CFE=45����OG=1�����߶� EF �ij���
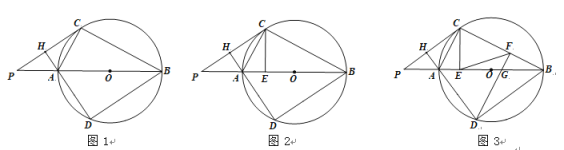
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���M������ԭ��O�ҷֱ�x�ᡢy���ڵ�A��B����CΪ��һ�����ڡ�M��һ�㣮����A��6��0������BCO��30����
��1�����B�����ꣻ
��2������D������Ϊ��-2��0�����Բ���ֱ��DB���M��λ�ù�ϵ����˵�����ɣ�
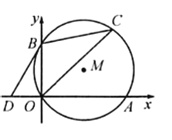
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com