
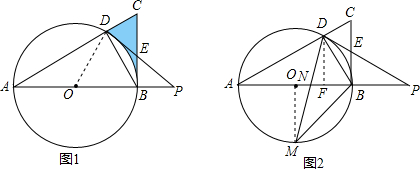
分析 (1)如图1,作辅助线;要证明PD是⊙O的切线,只要证明∠PDO=90°,运用切线的判定定理,即可解决问题.
(2)如图2,直接求出$\frac{DN}{MN}$的值,非常困难;因此,需要作辅助线,构造相似三角形;运用已知条件tan∠A=$\frac{1}{2}$,结合图形,联想勾股定理,设出参数(BD=x),求出AB的长度;进而求出DF的长度;运用△OMN∽△FDN,得到$\frac{DN}{MN}=\frac{DF}{OM}$,即可解决问题.
解答  解:(1)连结OD;
解:(1)连结OD;
∵AB是⊙O的直径,
∴∠ADB=90°,OA=OB,∠A+∠ABD=90°;
又∵OA=OB=OD,
∴∠ADO=∠A,∠BDO=∠ABD;
又∵∠A=∠PDB,
∴∠PDB+∠BD0=90°,
即∠PDO=90°,且D在圆上,
∴PD是⊙O的切线.
(2)∵BD=BP,
∴∠BDP=∠BPD;而∠ODP=90°,
∴∠ODB=∠DOB,
∴BD=BO=OD,△OBD为等边三角形,
∴∠DOB=60°,∠DBC=30°;
∵AB为⊙O的直径,
∴∠BDC=∠ADB=90°,而∠DBC=30°,
∴tan30°=$\frac{DC}{BD}$,cos30°=$\frac{BD}{BC}$,而BD=2$\sqrt{3}$,
∴DC=2,BC=4;
∵$\widehat{BD}$=$\frac{60π•2\sqrt{3}}{180}$=$\frac{2\sqrt{3}π}{3}$,
∴曲边三角形(阴影部分)的周长为:6+$\frac{2\sqrt{3}π}{3}$.
(3)连结OM,过D作DF⊥AB于F;
∵点M是$\widehat{AB}$ 的中点,
∴OM⊥AB;设BD=x,
∵tan∠A=$\frac{BD}{AD}$=$\frac{1}{2}$,
∴AD=2x;由勾股定理得:
AB=$\sqrt{(2x)^{2}+{x}^{2}}$=$\sqrt{5}x$;由三角形的面积公式得:$\frac{1}{2}$AD•BD=$\frac{1}{2}$AB•DF,
∴DF=$\frac{2\sqrt{5}}{5}x$;
∵OM∥DF,
∴△OMN∽△FDN,
∴$\frac{DN}{MN}=\frac{DF}{OM}$,DF=$\frac{2\sqrt{5}}{5}x$,OM=$\frac{\sqrt{5}}{2}x$,
∴$\frac{DN}{MN}=\frac{4}{5}$.
点评 该题以圆为载体,以考查切线的判定、等边三角形的判定及其性质、弧长公式、勾股定理、相似三角形的判定等几何知识点及其应用为核心构造而成;解题的方法是深入观察图形,数形结合,准确找出图形中隐含的相等或相似关系;解题的关键是牢固掌握等边三角形的判定及其性质、弧长公式、勾股定理等几何知识点.


科目:初中数学 来源: 题型:填空题
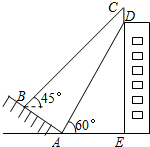 如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为5.4米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为5.4米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com