
����Ŀ������ѧϰ�����Ĺ����뷽����̽������![]()
![]() ��ͼ�������ʣ���Ϊ
��ͼ�������ʣ���Ϊ![]() ����
����![]() ���������ǶԱȺ���
���������ǶԱȺ���![]() ��̽����
��̽����
���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��㣺��ƽ��ֱ������ϵ�У����Ա���![]() ��ȡֵΪ�����꣬��
��ȡֵΪ�����꣬��![]() ��Ӧ�ĺ���ֵΪ�����꣬�����Ӧ�ĵ㣬��ͼ��ʾ��
��Ӧ�ĺ���ֵΪ�����꣬�����Ӧ�ĵ㣬��ͼ��ʾ��
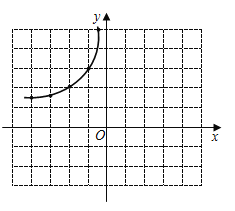
��1���벹ȫ����ͼ��
��2���۲�ͼ�������ش��������⣺
�ٵ�![]() ʱ��
ʱ��![]() ��
��![]() �������_________�������������
�������_________�������������
��![]() ��ͼ������
��ͼ������![]() ��ͼ����________ƽ��________����λ���õ���
��ͼ����________ƽ��________����λ���õ���
��ͼ����ڵ�_________���ĶԳƣ����������꣩
��3����Ϻ���ͼ��![]() ʱ����
ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1������⣻��2�������ϣ�1����0��1������3����1��x��0��x��1
��������
��1���ù⻬����˳�����Ӽ��ɣ�
��2������ͼ���ɽ�����⣻
��3���������������A��B�����꣬�ɴ˼��ɽ�����⣮
�⣺��1������ͼ����ͼ��ʾ��
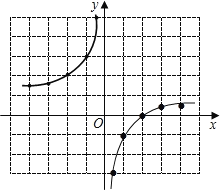
��2������x��0ʱ��y��x�����������
��![]() ��ͼ������y��
��ͼ������y��![]() ��ͼ������ƽ��1����λ���õ���
��ͼ������ƽ��1����λ���õ���
��ͼ����ڵ㣨0��1�����ĶԳƣ�
�ʴ�Ϊ�������ϣ�1����0��1����
��3����������ã�![]() ����2x+1����ã�x����1��
����2x+1����ã�x����1��
��x��1ʱ��y����2x+1����1��
��x����1ʱ��y����2x+1��3��
�ཻ��Ϊ��1����1��������1��3����
�൱![]() ����2x+1ʱ����x��ȡֵ��ΧΪ��1��x��0��x��1��
����2x+1ʱ����x��ȡֵ��ΧΪ��1��x��0��x��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧͼ��ݽ��չ����ס�������ͼ�飬ÿ������ͼ��Ľ��۱�ÿ������ͼ��Ľ��۸�20Ԫ����780Ԫ��������ͼ��������뻨540Ԫ��������ͼ���������ͬ��
��1����ס�������ͼ��ÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2��������ѧ�����ס�������ͼ�鹲70�����ܹ�����ò�����3950Ԫ������������ͼ����ٱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�����Ҳ�������˵������һ����ѧ���⣬�ı�������ʽ���任���Ľṹ��ֱ�������м�ֵ�Ķ�����������ѧ�����һ����Ҫԭ��
�Ķ�����������ϣ��ش�����
����һ��ƽ������Ϳ��������ǻ������㣬�磺a2��2ab+b2����a��b��2����ô![]() ��|a��b|����ô��ν�˫�ض��θ�ʽ
��|a��b|����ô��ν�˫�ض��θ�ʽ![]() ��a��0��b��0��a��2
��a��0��b��0��a��2![]() ��0�������أ������ҵ�������m��n��m��0��n��0����ʹ�ã�
��0�������أ������ҵ�������m��n��m��0��n��0����ʹ�ã�![]() 2+��
2+��![]() ��2��a��m+n��a����ʹ
��2��a��m+n��a����ʹ![]() ��mn��b����ôa��2
��mn��b����ôa��2![]() ����
����![]() ��2+��
��2+��![]() ��2��2
��2��2![]() ����
����![]() 2
2
��![]() ��
��![]() ��
��![]() |��˫�ض��θ�ʽ���Ի���
|��˫�ض��θ�ʽ���Ի���
���绯��![]() ����3��1+2��2��1��2����3+2
����3��1+2��2��1��2����3+2![]() ����
����![]() ��2+��
��2+��![]() ��2+2
��2+2![]() ��
��
��![]() ��
��![]() ��1+
��1+![]() ��
��
���϶�����ֱ������ϵxoy�У����ڵ�P��x��y����Q��x��y���������¶��壺��y����![]() ����Ƶ�QΪ��P�ġ��Ḻ�ݱ�㡱���磬�㣨3��2���ġ��Ḻ�ݱ�㡱Ϊ��3��2�����㣨��2��5���ġ��Ḻ�ݱ�㡱Ϊ����2����5��
����Ƶ�QΪ��P�ġ��Ḻ�ݱ�㡱���磬�㣨3��2���ġ��Ḻ�ݱ�㡱Ϊ��3��2�����㣨��2��5���ġ��Ḻ�ݱ�㡱Ϊ����2����5��
���⣺
��1����ֱ��д���㣨��3![]() ����2���ġ��Ḻ�ݱ�㡱Ϊ�� ��������
����2���ġ��Ḻ�ݱ�㡱Ϊ�� ��������![]() ���� ����
���� ����
��2����MΪһ�κ���y����x+1ͼ���ϵĵ㣬M��Ϊ��M�ĺḺ�ݱ�㣬��֪N��1��1������M��N��![]() �����M�����ꣻ
�����M�����ꣻ
��3����֪bΪ������1��b��2����P�ں���y����x2+16��![]() +����
+����![]() ��7��x��a����ͼ���ϣ��䡰�Ḻ�ݱ�㡱��������y����ȡֵ��Χ�ǩ�32��y���32����aΪż������a��ֵ��
��7��x��a����ͼ���ϣ��䡰�Ḻ�ݱ�㡱��������y����ȡֵ��Χ�ǩ�32��y���32����aΪż������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��2ax��2��ͼ��Ϊ������C1������ΪM��ֱ��l��y��2x��a��x�ᣬy��ֱ���A��B��
��1������������C1�����½�����ȷ������ ����
���Գ����ǣ�ֱ��x��1�����������꣨1����a��2������������һ�������������㣮
��2����a��0ʱ�����ABM�����ΪS����S��a�ĺ�����ϵ��
��3�������κ���y��ax2��2ax��2��ͼ��C1�Ƶ�P��t����2����ת180��õ����κ�����ͼ��Ϊ������C2��������ΪN��
������2��x��1ʱ����תǰ����������κ���y��ֵ������x���������С����t��ȡֵ��Χ��
����a��1ʱ����Q��������C1�ϵ�һ�㣬��Q��������C2�ϵĶ�Ӧ��ΪQ'����̽���ı���QMQ'N�ܷ�Ϊ�����Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ҹ����δ������ɽ��ҹ����������Ǭ¡ʱ�ھ�������������ʱ�ΰ���֪������������Ϊ����ʮ����֮һ�ڳ�������ͷ�����������������������꽭��������������ҹ����һ��������Ŀ��һ���ִ��ӳ�������ͷ����������ʻ��![]() Сʱ��һ��ͧҲ�ӳ�������ͷ������ͬһ��·������ʻ������ͧ�ȵ���Ŀ�ĵغ����̰�ԭ�ٷ��ز���;�����ִ��ڶ������������ִ���ʻ��ʱ��Ϊ
Сʱ��һ��ͧҲ�ӳ�������ͷ������ͬһ��·������ʻ������ͧ�ȵ���Ŀ�ĵغ����̰�ԭ�ٷ��ز���;�����ִ��ڶ������������ִ���ʻ��ʱ��Ϊ![]()
![]() ����ͧ���ִ�֮��ľ���Ϊ
����ͧ���ִ�֮��ľ���Ϊ![]() ��
��![]() ��
��![]() �ĺ�����ϵʽ��ͼ��ʾ�����ͧ���ִ��ڶ�������ʱ����������ͷ�ľ���Ϊ_____ǧ�ף�
�ĺ�����ϵʽ��ͼ��ʾ�����ͧ���ִ��ڶ�������ʱ����������ͷ�ľ���Ϊ_____ǧ�ף�
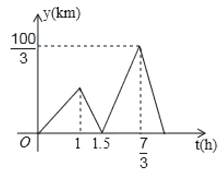
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ��� y=ax2+bx+c ��ͼ���� x ��Ľ���ĺ�����ֱ�Ϊ-1��3����
��ac��0����2a+b=0����4a+2b+c��0������������ x ���� ax2+bx��a+b�����н�����ȷ�ĸ������� ��
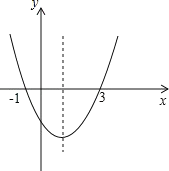
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ�ۺ�ʵ���С���ͬѧ����������һ����DE�ĸ߶ȣ����������������ǰ��һ��¥ͤǰ��̨����A�㴦���������D������Ϊ30��������������ķ����ߵ�̨���µĵ�C�������������D������Ϊ60������֪A��ĸ߶�ABΪ3�ף�̨��AC���¶�Ϊ1��![]() ����AB��BC=1��
����AB��BC=1��![]() ������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ�
������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
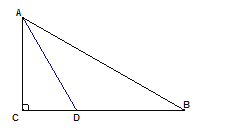
����Ŀ����֪����ͼ����Rt��ABC�У���C=90����BAC�Ľ�ƽ����AD��BC����D��
��1����AB����һ��OΪԲ������O��ʹ����A��D���㣨��д������������ͼ�ۼ��������ж�ֱ��BC����O��λ�ù�ϵ����˵�����ɣ�
��2������1���е���O��AB�ߵ���һ������ΪE��AB=3![]() ��BD=3,���߶�BD��BE���ӻ�DE��Χ�ɵ�ͼ�������������������ź�
��BD=3,���߶�BD��BE���ӻ�DE��Χ�ɵ�ͼ�������������������ź�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD�У���B��60��������P��ÿ��1����λ���ٶ��Ե�A�������߶�AB�˶�����B��ͬʱ����Q��ÿ��2����λ���ٶ��Ե�B����������B��C��D�˶�����D��ͼ2�ǵ�P��Q�˶�ʱ����BPQ�����S��ʱ��t�仯��ϵͼ����a��ֵ�ǣ�������
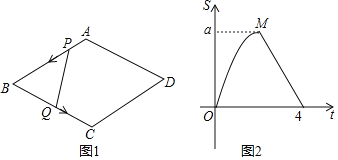
A.2B.2.5C.3D.2![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com