
【题目】著名数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则.”
阅读下列两则材料,回答问题
材料一:平方运算和开方运算是互逆运算,如:a2±2ab+b2=(a±b)2,那么![]() =|a±b|,那么如何将双重二次根式
=|a±b|,那么如何将双重二次根式![]() (a>0,b>0,a±2
(a>0,b>0,a±2![]() >0)化简呢?如能找到两个数m,n(m>0,n>0),使得(
>0)化简呢?如能找到两个数m,n(m>0,n>0),使得(![]() 2+(
2+(![]() )2=a即m+n=a,且使
)2=a即m+n=a,且使![]() 即mn=b,那么a±2
即mn=b,那么a±2![]() =(
=(![]() )2+(
)2+(![]() )2±2
)2±2![]() =(
=(![]() 2
2
∴![]() =
=![]() =
=![]() |,双重二次根式得以化简.
|,双重二次根式得以化简.
例如化简:![]() .∵3=1+2且2=1×2,∴3+2
.∵3=1+2且2=1×2,∴3+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() ,
,
∴![]() =
=![]() =1+
=1+![]() .
.
材料二:在直角坐标系xoy中,对于点P(x,y)和Q(x,y′)出如下定义:若y′=![]() ,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
问题:
(1)请直接写出点(﹣3![]() ,﹣2)的“横负纵变点”为 ;化简
,﹣2)的“横负纵变点”为 ;化简![]() = ;
= ;
(2)点M为一次函数y=﹣x+1图象上的点,M′为点M的横负纵变点,已知N(1,1),若M′N=![]() ,求点M的坐标;
,求点M的坐标;
(3)已知b为常数且1≤b≤2,点P在函数y=﹣x2+16(![]() +)(
+)(![]() ﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
【答案】(1)(﹣3![]() ,2);
,2);![]() ﹣
﹣![]() ;(2)当a≥0时,M'(3,﹣2);当a<0时,M'(﹣1,﹣2);(3)a=4或a=6
;(2)当a≥0时,M'(3,﹣2);当a<0时,M'(﹣1,﹣2);(3)a=4或a=6
【解析】
(1)﹣3![]() <0,得到(﹣3
<0,得到(﹣3![]() ,﹣2)的“横负纵变点”为(﹣3
,﹣2)的“横负纵变点”为(﹣3![]() ,2);
,2);![]() =
=![]() =
=![]() ﹣
﹣![]() ;
;
(2)设点M(a,1﹣a),当a≥0时,M'(a,1﹣a),M'(3,﹣2);当a<0时,M'(a,a﹣1),M'(﹣1,﹣2);
(3)![]()
![]() =
=![]() +1+1﹣
+1+1﹣![]() =2,令y'=
=2,令y'=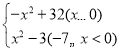 ,当﹣7≤x<0时,﹣32<y'≤17,当x≥0时,y'≤32,即可求出a.
,当﹣7≤x<0时,﹣32<y'≤17,当x≥0时,y'≤32,即可求出a.
解:(1)∵﹣3![]() <0,根据“横负纵变点”的定义,
<0,根据“横负纵变点”的定义,
∴(﹣3![]() ,﹣2)的“横负纵变点”为(﹣3
,﹣2)的“横负纵变点”为(﹣3![]() ,2);
,2);
![]() =
=![]() =
=![]() ﹣
﹣![]() ;
;
故答案为:(﹣3![]() ,2);
,2);![]() ﹣
﹣![]() ;
;
(2)设点M(a,1﹣a),
当a≥0时,M'(a,1﹣a),
∵N(1,1),M′N=![]() ,
,
∴(1﹣a)2+a2=13,
∴a=3或a=﹣2(舍),
∴M'(3,﹣2);
当a<0时,M'(a,a﹣1),
∵N(1,1),M′N=![]() ,
,
∴(1﹣a)2+(2﹣a)2=13,
∴a=﹣1或a=4(舍),
∴M'(﹣1,﹣2);
(3)∵1≤b≤2,∴0≤b﹣1≤1,
∵![]()
![]() =
=![]() +1+1﹣
+1+1﹣![]() =2,
=2,
∴y=﹣x2+32,
∴y'=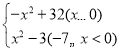 ,
,
当﹣7≤x<0时,﹣32<y'≤17;
当x≥0时,y'≤32;
令﹣x2+32=17,解得x1=![]() 或x2=﹣
或x2=﹣![]() (舍);
(舍);
令﹣x2+32=﹣32,解得x1=8或x2=﹣8(舍);
∴![]() ≤a<8,
≤a<8,
∵a是偶数,
∴a=4或a=6.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=![]() ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
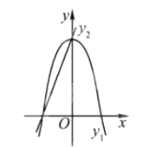
【题目】如图,已知抛物线![]() ,直线
,直线![]() ,当
,当![]() 任取一值时,
任取一值时,![]() 对应的函数值分别 为
对应的函数值分别 为![]() ,若
,若![]() ,取
,取![]() 中的较小值记为
中的较小值记为![]() ;若
;若![]() ,记
,记![]() ,例如:当
,例如:当![]() 时,
时,![]() ,此时
,此时![]() ,下列判断:
,下列判断:
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() 值越大,
值越大,![]() 值越小;
值越小;
③使得![]() 大于2的
大于2的![]() 值不存在;
值不存在;
④使得![]() 的
的![]() 值是
值是![]() 或
或![]() .
.
其中正确的是_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形OABC中,OA=4,OC=2,以点O为坐标原点,OA所在的直线为x轴,建立直角坐标系.
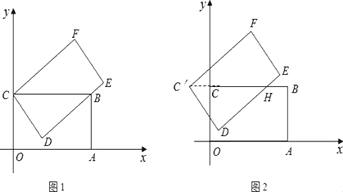
(1)将矩形OABC绕点C逆时针旋转至矩形DEFC,如图1,DE经过点B,求旋转角的大小和点D,F的坐标;
(2)将图1中矩形DEFC沿直线BC向左平移,如图2,平移速度是每秒1个单位长度.
①经过几秒,直线EF经过点B;
②设两矩形重叠部分的面积为S,运动时间为t,写出重叠部分面积S与时间t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
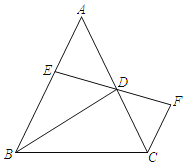
【题目】已知:如图,在△ABC中AB=AC,BD平分∠ABC交AC于点D,DE平分∠ADB交AB于点E,CF∥AB交ED的延长线于F,若∠A=52°,求∠DFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.
(1)求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?
(2)学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
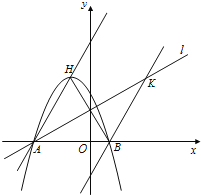
【题目】如图,抛物线y=mx![]() +2mx-3m(m≠0)的顶点为H,与
+2mx-3m(m≠0)的顶点为H,与![]() 轴交于A、B两点(B点在A点右侧),点H、B关于直线l:
轴交于A、B两点(B点在A点右侧),点H、B关于直线l:![]() 对称,过点B作直线BK∥AH交直线l于K点.
对称,过点B作直线BK∥AH交直线l于K点.
(1)求A、B两点坐标,并证明点A在直线I上。
(2)求此抛物线的解析式;
(3)将此抛物线向上平移,当抛物线经过K点时,设顶点为N,求出NK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]()
![]() 的图象与性质.因为
的图象与性质.因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
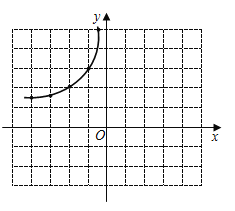
(1)请补全函数图象;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而_________;(填“增大”或“减小”)
的增大而_________;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向________平移________个单位而得到;
的图象向________平移________个单位而得到;
③图象关于点_________中心对称.(填点的坐标)
(3)结合函数图象,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
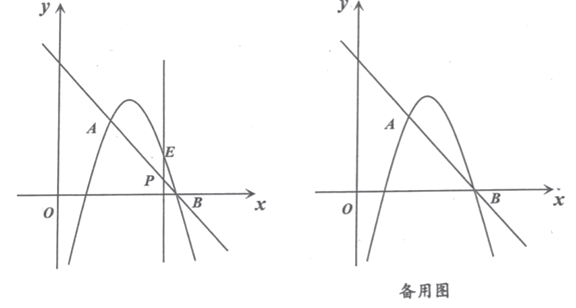
【题目】抛物线![]() 直线
直线![]() 一个交点
一个交点![]() 另一个交点
另一个交点![]() 在
在![]() 轴上,点
轴上,点![]() 是线段
是线段![]() 上异于
上异于![]() 的一个动点,过点
的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() .
.
(1)求抛物线的解析式;
(2)是否存在这样的点![]() ,使线段
,使线段![]() 长度最大?若存在,求出最大值及此时点
长度最大?若存在,求出最大值及此时点![]() 的坐标,若不存在,说明理由;
的坐标,若不存在,说明理由;
(3)求当![]() 为直角三角形时点P的坐标.
为直角三角形时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com