
【题目】在矩形OABC中,OA=4,OC=2,以点O为坐标原点,OA所在的直线为x轴,建立直角坐标系.
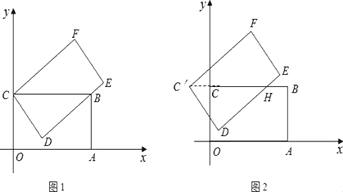
(1)将矩形OABC绕点C逆时针旋转至矩形DEFC,如图1,DE经过点B,求旋转角的大小和点D,F的坐标;
(2)将图1中矩形DEFC沿直线BC向左平移,如图2,平移速度是每秒1个单位长度.
①经过几秒,直线EF经过点B;
②设两矩形重叠部分的面积为S,运动时间为t,写出重叠部分面积S与时间t之间的函数关系式.
【答案】(1)旋转角为30°,D(1,![]() ),F(
),F(![]() ;(2)①直线EF经过点B时所需的时间为
;(2)①直线EF经过点B时所需的时间为![]() 秒;②当0<t<1时,
秒;②当0<t<1时,![]() ;当1≤t<4时,
;当1≤t<4时,![]() .
.
【解析】
(1)根据OA=4,OC=2,可得BC=2CD,则可以求出∠BCD=60°,则旋转角即可求得;作DM⊥CB于点M,FN⊥CB于点N,根据三角函数即可求得DM,CM的长,从而求得D的坐标,在Rt△CFN中,根据三角函数求得CN,FN的长,即可得F的坐标;
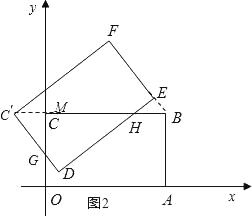
(2)①如图,HB即为直线EF经过点B时移动的距离,在Rt△C′DH中利用三角函数即可求得DH,从而得到HE,再在Rt△HEB中,利用三角函数求得BH,即可求得时间;
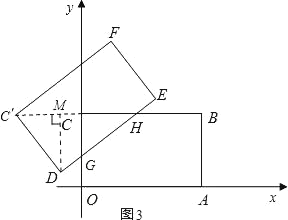
②分两种情况进行讨论:当0<t<1时,重叠部分面积为四边形DGCH,如图2;当1≤t<4时,重叠部分的面积为△GCH,如图3,分别求解即可.
解:(1)如图1,在矩形OABC中,OA=4,OC=2,
∴在Rt△BCD中,BC=2CD,即![]() ,
,
∴∠BCD=60°,
∴旋转角∠OCD=30°,
作DM⊥CB于点M,FN⊥CB于点N,
在Rt△CDM中,CM=CDcos60°=1,DM=CDsin60°=![]() ,
,
∴点D到x轴的距离为![]() ,
,
在Rt△CFN中,![]() ,
,
∴点F到x轴的距离为4,
故D(1,![]() ),F(
),F(![]() ,
,![]() );
);
(2)①如图2,HB即为直线EF经过点B时移动的距离,
在Rt△C′DH中,![]() ,
,
∴![]() ,
,
在Rt△BEH中,∠BHE=∠C′HD=30°,cos30°=![]() ,则
,则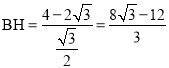 ,
,
∴直线EF经过点B时所需的时间为![]() 秒;
秒;
②过点D作DM⊥BC于点M,
在Rt△DMC′中,C′M=![]() ,
,
当0<t<1时,重叠部分面积为四边形DGCH,如图2,
∵C′C=t,CG=C′C·tan60°=![]() ,
,
∴![]() ,
,
当1≤t<4时,重叠部分的面积为△GCH,如图3,
∵![]() ,
,
∴![]() .
.



 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】两位同学在足球场上游戏,两人的运动路线如图1所示,其中AC=DB,小王从点A出发沿线段AB运动到点B,小林从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示,结合图象分析,下列说法正确的是( )
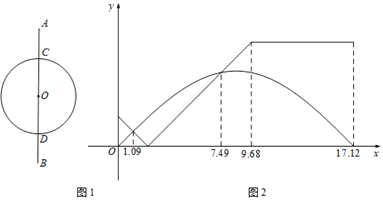
A. 小王的运动路程比小林的长
B. 两人分别在![]() 秒和
秒和![]() 秒的时刻相遇
秒的时刻相遇
C. 当小王运动到点D的时候,小林已经过了点D
D. 在![]() 秒时,两人的距离正好等于
秒时,两人的距离正好等于![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宣和中学图书馆今日购进甲、乙两种图书,每本甲种图书的进价比每本乙种图书的进价高20元,花780元购进甲种图书的数量与花540元购进乙种图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元;
(2)宣和中学购进甲、乙两种图书共70本,总购书费用不超过3950元,则最多购进甲种图书多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的高,且
的高,且![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,点E在AD上,连接![]() ,将
,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若BE=BC,求
,若BE=BC,求![]() 的大小;
的大小;
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
图1.  图2.
图2.  图3.
图3. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组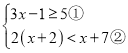
请结合题意,完成本题的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
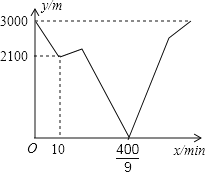
【题目】已知A、B两地之间的路程为3000m,甲、乙两人分别从A、B两地同时出发,相向而行,甲到B地停止,乙到A地停止,出发10分钟后,甲原路原速返回A地取重要物品,取到该物品后立即原路原速前往B地(取物品的时间忽略不计),结果到达B地的时间比乙到达A地的时间晚,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(m)与甲运动的时间x(min)之间的关系如图所示,则乙到达A地时,甲与B地相距的路程是_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则.”
阅读下列两则材料,回答问题
材料一:平方运算和开方运算是互逆运算,如:a2±2ab+b2=(a±b)2,那么![]() =|a±b|,那么如何将双重二次根式
=|a±b|,那么如何将双重二次根式![]() (a>0,b>0,a±2
(a>0,b>0,a±2![]() >0)化简呢?如能找到两个数m,n(m>0,n>0),使得(
>0)化简呢?如能找到两个数m,n(m>0,n>0),使得(![]() 2+(
2+(![]() )2=a即m+n=a,且使
)2=a即m+n=a,且使![]() 即mn=b,那么a±2
即mn=b,那么a±2![]() =(
=(![]() )2+(
)2+(![]() )2±2
)2±2![]() =(
=(![]() 2
2
∴![]() =
=![]() =
=![]() |,双重二次根式得以化简.
|,双重二次根式得以化简.
例如化简:![]() .∵3=1+2且2=1×2,∴3+2
.∵3=1+2且2=1×2,∴3+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() ,
,
∴![]() =
=![]() =1+
=1+![]() .
.
材料二:在直角坐标系xoy中,对于点P(x,y)和Q(x,y′)出如下定义:若y′=![]() ,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
问题:
(1)请直接写出点(﹣3![]() ,﹣2)的“横负纵变点”为 ;化简
,﹣2)的“横负纵变点”为 ;化简![]() = ;
= ;
(2)点M为一次函数y=﹣x+1图象上的点,M′为点M的横负纵变点,已知N(1,1),若M′N=![]() ,求点M的坐标;
,求点M的坐标;
(3)已知b为常数且1≤b≤2,点P在函数y=﹣x2+16(![]() +)(
+)(![]() ﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
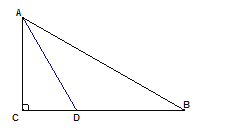
【题目】已知,如图,在Rt△ABC中,∠C=90,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心作⊙O,使它过A,D两点(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=3![]() ,BD=3,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和
,BD=3,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com