
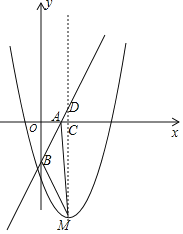
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
【答案】(1)①②③;(2)S=a(a>0);(3)①![]() ;②t=﹣2或1或4.
;②t=﹣2或1或4.
【解析】
(1)二次函数y=ax2﹣2ax﹣2的对称轴为x=![]() =1,y=ax2﹣2ax﹣2=a(x2﹣2x)﹣2,即可求解;
=1,y=ax2﹣2ax﹣2=a(x2﹣2x)﹣2,即可求解;
(2)由S=S△BMD﹣S△AMD=![]() MD(OC﹣AC),即可求解;
MD(OC﹣AC),即可求解;
(3)①而x=1和x=m关于P(t,﹣2)中心对称,所以P到这两条对称轴的距离相等,则1﹣t=t﹣m,m=2t﹣1,且:2t﹣1≤﹣2,即可求解;②分t≤1、t>1两种情况求解即可.
解:(1)二次函数y=ax2﹣2ax﹣2的对称轴为x=![]() =1,
=1,
当x=1时,y=﹣a﹣2;
y=ax2﹣2ax﹣2=a(x2﹣2x)﹣2,即当x=0或2时,抛物线过定点,即(0,﹣2)、(2,﹣2),
故答案为:①②③;
(2)由抛物线的顶点公式求得:顶点M(1,﹣a﹣2)
当x=1时,y=2×1﹣a=2﹣a,求得:D(1,2﹣a)
当y=0时,0=2x﹣a,x=![]() a,求得:A(a/2,0)
a,求得:A(a/2,0)
∴DM=2﹣a﹣(﹣a﹣2)=4,
S=S△BMD﹣S△AMD=![]() MD(OC﹣AC)=
MD(OC﹣AC)=![]() ×4×
×4×![]() a=a(a>0),
a=a(a>0),
(3)①当﹣2≤x≤1时,
C1的y的值都会随x的增大而减小,而C1的对称轴为x=1,
﹣2≤x≤1在对称轴的左侧,C1开口向上,所以a>0;
同时C2的开口向下,而又要当﹣2≤x≤1时y的值都会随x的增大而减小,
所以﹣2≤x≤1要在C2的对称轴右侧,
令C2的对称轴为x=m,则m≤﹣2,
而x=1和x=m关于P(t,﹣2)中心对称,所以P到这两条对称轴的距离相等,
所以:1﹣t=t﹣m,m=2t﹣1,且:2t﹣1≤﹣2,即:![]() ;
;
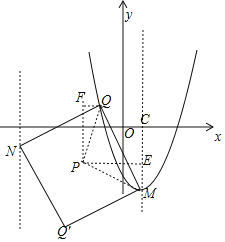
②当a=1时,M(1,﹣3),作PE⊥CM于E,将Rt△PME绕P旋转180°,得到Rt△PQF,
则△MPQ为等腰直角三角形,因为N、Q′是中心对称点,所以四边形MQNQ′为正方形.
第一种情况,当t≤1时,
PE=PF=1﹣t,ME=QF=1,CE=2,
∴Q(t+1,﹣t﹣1),
把Q(t+1,﹣t﹣1)代入y=x2﹣2x﹣2
﹣t﹣1=(t+1)2﹣2(t+1)﹣2,
t2+t﹣2=0,
解得:t1=1,t2=﹣2;
第二种情况,当t>1时,
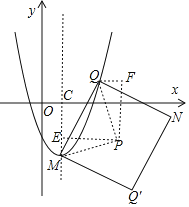
PE=PE=t﹣1,ME=QF=1,CE=2,
∴Q(t﹣1,t﹣3)代入:y=x2﹣2x﹣2,
t﹣3=(t﹣1)2﹣2(t﹣1)﹣2,
t2﹣5t+4=0,
解得:t1=1 (舍去),t2=4
综上:t=﹣2或1或4.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
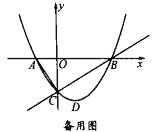
【题目】已知在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
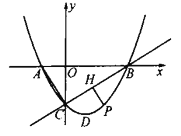
(1)如图,直线![]() 下方抛物线上的一个动点
下方抛物线上的一个动点![]() (不与点
(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() 最大时,点
最大时,点![]() 为线段
为线段![]() 一点(不与点
一点(不与点![]() 重合),当
重合),当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(2)将![]() 沿直线
沿直线![]() 翻折得
翻折得![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,在旋转过程中直线
,在旋转过程中直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:数学课上,老师出示了这样一个问题:
如图1,在等边![]() 中,点
中,点![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 延长线于
延长线于![]() 点,且
点,且![]() ,探究线段
,探究线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察和度量,发现图1中有一条线段与![]() 相等”;
相等”;
小伟:“通过构造三角形,证明三角形全等,进而可以得到线段![]() 之间的数量关系”.
之间的数量关系”.
……
老师:“保留原题条件,再过点![]() 作
作![]() 交
交![]() 于
于![]() 与
与![]() 相交于点
相交于点![]() (如图2)如果给出
(如图2)如果给出![]() 的值,那么可以求出
的值,那么可以求出![]() 的值”.
的值”.
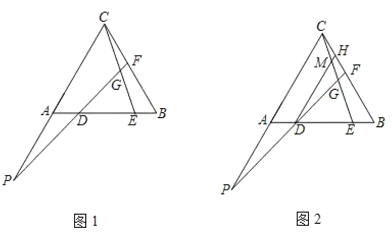
请回答:
(1)在图1中找出![]() 与
与![]() 数量关系,并证明;
数量关系,并证明;
(2)在图1中找出与线段![]() 相等的线段,并证明;
相等的线段,并证明;
(3)探究线段![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(4)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
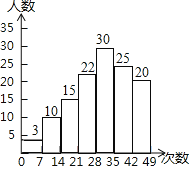
A.这栋居民楼共有居民125人
B.每周使用手机支付次数为28~35次的人数最多
C.有的人每周使用手机支付的次数在35~42次
D.每周使用手机支付不超过21次的有15人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
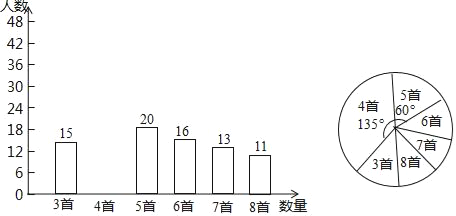
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上运动,且
上运动,且![]() .连接
.连接![]() ,作
,作![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .
.
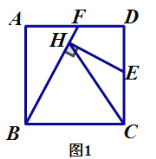

(1)如图1,若点![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 之间的数量关系是______;
之间的数量关系是______;
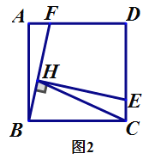
(2)如图2,当点![]() 在
在![]() 边上且不是
边上且不是![]() 的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上运动时,连接
上运动时,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 点从
点从![]() 点以1个单位/秒的速度向
点以1个单位/秒的速度向![]() 点运动,远动到
点运动,远动到![]() 点即停止,经过
点即停止,经过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为一边在
为一边在![]() 一侧作正方形
一侧作正方形![]() ,在
,在![]() 点运动过程中,设正方形
点运动过程中,设正方形![]() 与
与![]() 的重叠面积为
的重叠面积为![]() ,运动时间为
,运动时间为![]() 秒,如图2是
秒,如图2是![]() 与
与![]() 的函数图象.
的函数图象.
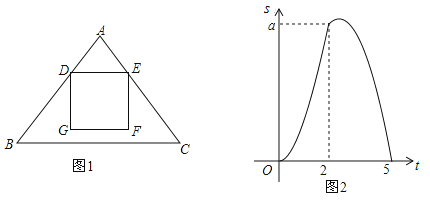
(1)求![]() 的长;
的长;
(2)求![]() 的值;
的值;
(3)求![]() 与
与![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程![]()
(1)求证:m取任何值时,方程总有实根.
(2)若二次函数![]() 的图像关于y轴对称.
的图像关于y轴对称.
a、求二次函数![]() 的解析式
的解析式
b、已知一次函数![]() ,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值
,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值![]() 均成立.
均成立.
(3)在(2)的条件下,若二次函数![]() 的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值
的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值![]() 均成立,求二次函数
均成立,求二次函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
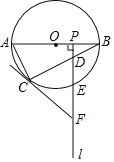
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,点
上一点,点![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,在射线
两点,在射线![]() 上取点
上取点![]() ,使
,使![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)当点![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com