
【题目】正方形![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上运动,且
上运动,且![]() .连接
.连接![]() ,作
,作![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .
.
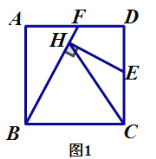

(1)如图1,若点![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 之间的数量关系是______;
之间的数量关系是______;
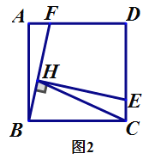
(2)如图2,当点![]() 在
在![]() 边上且不是
边上且不是![]() 的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
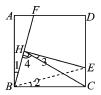
(3)如图3,当点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上运动时,连接
上运动时,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
【答案】(1)![]() ;(2)成立,证明见解析;(3)
;(2)成立,证明见解析;(3)![]() .
.
【解析】
(1)如图(见解析),连接BE,先根据正方形的性质、三角形全等的判定定理与性质得出![]() ,再根据圆周角定理得出
,再根据圆周角定理得出![]() ,从而可得
,从而可得![]() ,然后根据角互余得出
,然后根据角互余得出![]() ,最后根据等腰三角形的定义即可得;
,最后根据等腰三角形的定义即可得;
(2)如图(见解析),连接BE,先根据正方形的性质、三角形全等的判定定理与性质得出![]() ,再根据圆周角定理得出
,再根据圆周角定理得出![]() ,从而可得
,从而可得![]() ,然后根据角互余得出
,然后根据角互余得出![]() ,最后根据等腰三角形的定义即可得;
,最后根据等腰三角形的定义即可得;
(3)先根据角互余得出![]() ,再根据四边形的内角和、领补角定义得出
,再根据四边形的内角和、领补角定义得出![]() ,然后根据三角形全等的判定定理与性质得出
,然后根据三角形全等的判定定理与性质得出![]() ,又根据三角形全等的判定定理与性质得出
,又根据三角形全等的判定定理与性质得出![]() ,最后根据三角形的三边关系定理即可得.
,最后根据三角形的三边关系定理即可得.
(1)![]() ,证明如下:
,证明如下:
如图,连接BE
在正方形![]() 中,
中,![]() ,
,![]()
∵![]() ,
,![]()
∴![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,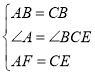
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() 、
、![]() 两点都在以
两点都在以![]() 为直径的圆上
为直径的圆上
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
又![]()
∴![]() ;
;

(2)(1)中的结论![]() 仍然成立,证明如下:
仍然成立,证明如下:
如图,连接![]()
在正方形![]() 中,
中,![]() ,
,![]()
∵![]() ,
,![]()
∴![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,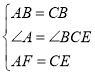
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() 、
、![]() 两点都在以
两点都在以![]() 为直径的圆上
为直径的圆上
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
又![]()
∴![]() ;
;
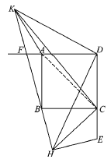
(3)如图,连接![]()
∵![]() ,
,![]()
∴![]()
∵![]()
![]()
![]()
![]()
![]()
又![]()
∴![]()
在![]() 和
和![]() 中,
中,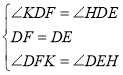
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,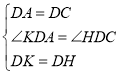
∴![]()
∴![]()
由(2)知,![]()
∴![]()
∵![]()
∴![]() ,
,![]()
在![]() 中,由三角形的三边关系定理得:
中,由三角形的三边关系定理得:![]()
∴当![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 的长最大,最大值为
的长最大,最大值为![]()
即线段![]() 长的最大值是
长的最大值是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交于
轴正半轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,且
,且![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④关于
;④关于![]() 的方程
的方程![]() 有一个根为
有一个根为![]() ,其中正确的结论个数有( )
,其中正确的结论个数有( )
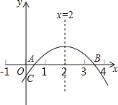
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:
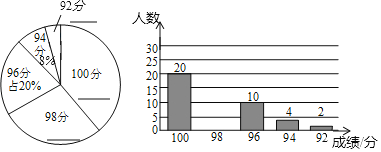
(1)计算样本中,成绩为98分的教师有 人,并补全两个统计图;
(2)样本中,测试成绩的众数是 ,中位数是 ;
(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完概率的有关内容后,小军与小波共同发明了一种利用“字母棋”进行比胜负的游戏,他们制作了5颗棋子,并在每颗棋子上标注相应的字母(棋子除了字母外,材质、大小、质地均相同),其中标有字母X的棋子有1颗,标有字母Y和Z的棋子分别有2颗.游戏规定:将5颗棋子放入一个不透明的袋子中,然后从5颗棋子中随机摸出两颗棋子,若摸到的两颗棋子标有字母X,则小军胜;若摸到两颗相同字母的棋子,则小波胜,其余情况为平局,则游戏重新进行.
(1)求随机摸到标有字母Y的棋子的概率;
(2)在游戏刚准备进行的同时,数学课代表小亮对游戏的公平性产生了质疑,请你通过列表法或者画树状图的方法帮小亮同学验证该游戏的规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
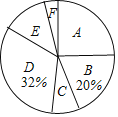
【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动.以下是根据调查结果绘制的统计图表的一部分.
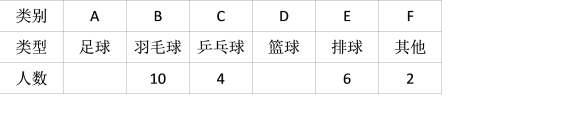
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜欢乒乓球的有 人,最喜欢篮球的学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,其中,最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %;
(3)该校共有450名学生,根据调查结果,估计该校最喜欢排球的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a、b、c.若b2+c2=2b+4c﹣5且a2=b2+c2﹣bc,则△ABC的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
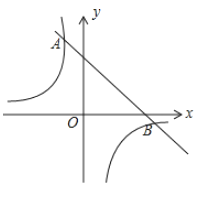
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)根据函数图象,直接写出满足![]() 的
的![]() 的取值范围是_______;
的取值范围是_______;
(2)求这两个函数的表达式;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com