
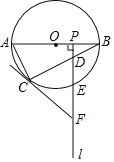
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,点
上一点,点![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,在射线
两点,在射线![]() 上取点
上取点![]() ,使
,使![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)当点![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)①四边形![]() 是菱形,理由见解析;②5.
是菱形,理由见解析;②5.
【解析】
(1)连接![]() ,利用
,利用![]() 和
和![]() 再进行等量代换证明OC⊥FC即可;
再进行等量代换证明OC⊥FC即可;
(2)①先证明![]() ,
,![]() 均为等边三角形,求得
均为等边三角形,求得![]() ,即可求解;
,即可求解;
②利用三角函数![]() ,和勾股定理求出AC,BC,再利用垂径定理求出HB,利用三角形面积公式求出PE,再求出OP,BP,DP即可.
,和勾股定理求出AC,BC,再利用垂径定理求出HB,利用三角形面积公式求出PE,再求出OP,BP,DP即可.
解:(1)证明:如图1,连接![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 是
是![]() 的切线.
的切线.
(2)如图2,连接![]() ,OE交CB于点H.
,OE交CB于点H.
①以![]() 为顶点的四边形是菱形.理由如下:
为顶点的四边形是菱形.理由如下:
![]() 是直径,
是直径,![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]()
![]() ,
,![]() 均为等边三角形,
均为等边三角形,
![]()
![]() 四边形
四边形![]() 是菱形;
是菱形;
②![]() ,设
,设![]() ,
,![]() ,
,
由勾股定理得![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,
∵AB=20,
∴OE=OB=10,
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
由勾股定理得![]() ,
,
![]() ,
,
![]() ,即
,即![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,求AB的长.
,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
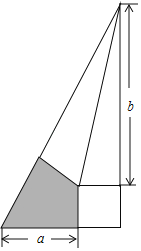
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,以点
,以点![]() 为顶点作
为顶点作![]() ,使得
,使得![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
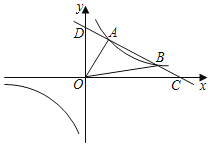
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校3月份开展网络授课教学,该校随机抽取部分学生,按四个类别(A、很喜欢;B、喜欢;C、一般;D、不喜欢;)统计它们对网络授课的接受情况,并将结果绘制成如下两幅不完整的统计图:
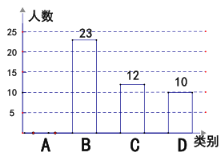
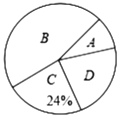
(1)这次共抽取_________名学生进行统计调查;扇形统计图中,D类所对应的扇形圆心角的大小为_______;
(2)将条形图补充完整;
(3)该校共有1500名学生,估计该校表示“喜欢”网络授课的B类的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
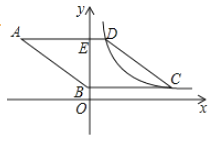
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(1)求出k值.
(2)求出△OCD的面积
(3)试探究坐标轴上是否存在点P,使得△PCD的面积等于菱形ABCD的面积的一半,如果存在,请直接写出点P的坐标;如不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com