
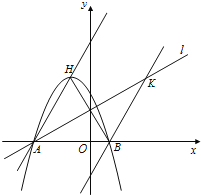
【题目】如图,抛物线y=mx![]() +2mx-3m(m≠0)的顶点为H,与
+2mx-3m(m≠0)的顶点为H,与![]() 轴交于A、B两点(B点在A点右侧),点H、B关于直线l:
轴交于A、B两点(B点在A点右侧),点H、B关于直线l:![]() 对称,过点B作直线BK∥AH交直线l于K点.
对称,过点B作直线BK∥AH交直线l于K点.
(1)求A、B两点坐标,并证明点A在直线I上。
(2)求此抛物线的解析式;
(3)将此抛物线向上平移,当抛物线经过K点时,设顶点为N,求出NK的长.
【答案】(1) A(-3,0) B(1,0) ; (2)y=-![]() x
x![]() -
-![]() x+
x+![]() ; (3)NK=4
; (3)NK=4![]()
【解析】
(1)令y=0,解关于x的一元二次方程,即可得到点A、B的坐标;然后把点A的坐标代入直线l的解析式,计算即可证明点A在直线上;
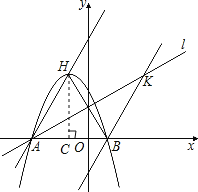
(2)根据轴对称的性质可得AH=AB,根据直线l的解析式求出直线l与x轴的夹角为30°,然后得到∠HAB的度数是60°,过点H作HC⊥x轴于点C,然后解直角三角形求出AC、HC,从而得到OC的长度,然后写出点H的坐标,再把点H的坐标代入抛物线解析式计算求出m的值,即可得解;
(3)根据平行直线的解析式的k值相等求出直线BK的解析式的k值,然后利用待定系数法求出直线BK的解析式,与直线l的解析式联立求解得到点K的值,再利用抛物线解析式求出相应横坐标上的点,从而求出抛物线向上移动的距离,然后得到平移后的抛物线的顶点N的坐标,根据两点间的距离公式计算即可得到NK的值.
令y=0,则mx2+2mx-3m=0(m≠0),
解得x1=-3,x2=1,
∵B点在A点右侧,
∴A点坐标为(-3,0),B点坐标为(1,0),
证明:∵直线l:![]()
当x=-3时,![]()
∴点A在直线l上;
(2)∵点H、B关于过A点的直线l:![]() 对称,
对称,
∴AH=AB=4,
设直线l与x轴的夹角为α,则![]()
所以,∠α=30°,
∴∠HAB=60°,
过顶点H作HC⊥AB交AB于C点,
则![]()
∴顶点H![]()
代入抛物线解析式,得![]()
解得m=-![]()
所以,抛物线解析式为![]()
(3)∵BK∥AH
∴直线BK的k=tan60°=![]()
设直线BK的解析式为y=![]() x+b,
x+b,
∵B点坐标为(1,0),
∴![]() +b=0,
+b=0,
解得b=-![]() ,
,
∴直线BK的解析式为y=![]() x-
x-![]()
联立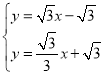
解得
∴点K的坐标为(3,2![]() ),
),
当x=3时,![]()
∴平移后与点K重合的点的坐标为(3,-6![]() ),
),
平移距离为2![]() -(-6
-(-6![]() )=8
)=8![]() ,
,
∵平移前顶点坐标为(-1,2![]() ),
),
2![]() +8
+8![]() =10
=10![]() ,
,
∴平移后顶点坐标N(-1,10![]() ),
),
![]()
所以,NK的长是4![]()


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】将矩形![]() 如图放置在平面直角坐标系中,
如图放置在平面直角坐标系中,![]() 为边
为边![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() ,且
,且![]() ,
,![]() 的长是方程
的长是方程![]() 的两个实数根,且
的两个实数根,且![]() .
.
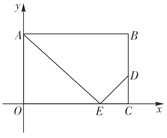
(1)设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系(不求
的函数关系(不求![]() 的取值范围);
的取值范围);
(2)当![]() 为
为![]() 的中点时,求直线
的中点时,求直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,平面内是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形?若存在,请直接写出点
为顶点的四边形为平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组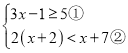
请结合题意,完成本题的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则.”
阅读下列两则材料,回答问题
材料一:平方运算和开方运算是互逆运算,如:a2±2ab+b2=(a±b)2,那么![]() =|a±b|,那么如何将双重二次根式
=|a±b|,那么如何将双重二次根式![]() (a>0,b>0,a±2
(a>0,b>0,a±2![]() >0)化简呢?如能找到两个数m,n(m>0,n>0),使得(
>0)化简呢?如能找到两个数m,n(m>0,n>0),使得(![]() 2+(
2+(![]() )2=a即m+n=a,且使
)2=a即m+n=a,且使![]() 即mn=b,那么a±2
即mn=b,那么a±2![]() =(
=(![]() )2+(
)2+(![]() )2±2
)2±2![]() =(
=(![]() 2
2
∴![]() =
=![]() =
=![]() |,双重二次根式得以化简.
|,双重二次根式得以化简.
例如化简:![]() .∵3=1+2且2=1×2,∴3+2
.∵3=1+2且2=1×2,∴3+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() ,
,
∴![]() =
=![]() =1+
=1+![]() .
.
材料二:在直角坐标系xoy中,对于点P(x,y)和Q(x,y′)出如下定义:若y′=![]() ,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
问题:
(1)请直接写出点(﹣3![]() ,﹣2)的“横负纵变点”为 ;化简
,﹣2)的“横负纵变点”为 ;化简![]() = ;
= ;
(2)点M为一次函数y=﹣x+1图象上的点,M′为点M的横负纵变点,已知N(1,1),若M′N=![]() ,求点M的坐标;
,求点M的坐标;
(3)已知b为常数且1≤b≤2,点P在函数y=﹣x2+16(![]() +)(
+)(![]() ﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
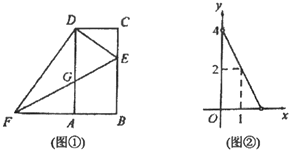
【题目】如图①,四边形![]() 是矩形,
是矩形,![]() ,点
,点![]() 是线段
是线段![]() 上一动点 (不与
上一动点 (不与![]() 重合),点
重合),点![]() 是线段
是线段![]() 延长线上一动点,连接
延长线上一动点,连接![]() 交
交![]() 于点
于点![]() .设
.设![]() ,已知
,已知![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
(1)求图②中![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)求证:![]() ;
;
(3)是否存在![]() 的值,使得
的值,使得![]() 是等腰三角形?如果存在,求出
是等腰三角形?如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
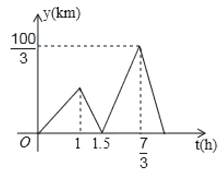
【题目】不览夜景,未到重庆山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,![]() 小时后一快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为
小时后一快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为![]()
![]() ,快艇和轮船之间的距离为
,快艇和轮船之间的距离为![]() ,
,![]() 与
与![]() 的函数关系式如图所示,则快艇与轮船第二次相遇时到朝天门码头的距离为_____千米.
的函数关系式如图所示,则快艇与轮船第二次相遇时到朝天门码头的距离为_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
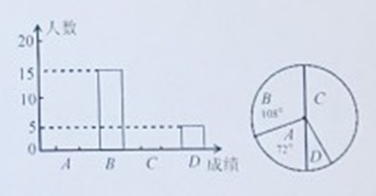
【题目】某校九年级体自模拟测试后,随机抽取了九年级部分学生体有测试成绩进行统计,得到相关的统计图表如下:
成绩/分 |
|
|
|
|
成绩等级 |
|
|
|
|
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的体育测试成绩,补全频数分布直方图
(2)扇形![]() 的圆心角的度数是
的圆心角的度数是
(3)若该校九年级有![]() 名学生,请据此估计该校九年级此次体育测试成绩在
名学生,请据此估计该校九年级此次体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生有多少人?
等级)的学生有多少人?
(4)根据测试中存在的问题,通过一段时间的针对性调练,若![]() 等级学生数可提高
等级学生数可提高![]() 等级学生数可提高
等级学生数可提高![]() ,请估计经过训练后九年级体育测试成绩在
,请估计经过训练后九年级体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生可达多少人?
等级)的学生可达多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com