
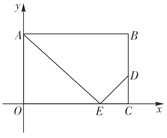
【题目】将矩形![]() 如图放置在平面直角坐标系中,
如图放置在平面直角坐标系中,![]() 为边
为边![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() ,且
,且![]() ,
,![]() 的长是方程
的长是方程![]() 的两个实数根,且
的两个实数根,且![]() .
.
(1)设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系(不求
的函数关系(不求![]() 的取值范围);
的取值范围);
(2)当![]() 为
为![]() 的中点时,求直线
的中点时,求直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,平面内是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形?若存在,请直接写出点
为顶点的四边形为平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在.
;(3)存在.![]() ,
,![]() ,
,![]() .
.
【解析】
(1)利用因式分解法解出一元二次方程,得到OA、OB的长,证明△AOE∽△ECD,根据相似三角形的性质列出比例式,整理得到y与x的函数关系;
(2)列方程求出OE,利用待定系数法求出直线AE的解析式;
(3)根据平行四边形的性质、坐标与图形性质解答.
(1)![]() ,
,
![]() ,
,
∴解得![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴∠AEO+∠DEC=90![]() ,
,
又∵∠AEO+∠OAE=90![]() ,
,
∴∠OAE=∠CED,又∠AOE=∠ECD=90![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)当![]() 为
为![]() 的中点时,
的中点时,![]() .
.
∵![]() ,
,
∴![]() .
.
解得![]() ,
,![]() .
.
当![]() 时,设直线
时,设直线![]() 的解析式为
的解析式为![]() ,把A(0,8),E(4,0)代入
,把A(0,8),E(4,0)代入
得![]()
解得![]() ,
,
∴![]() ;
;
当![]() 时,设直线
时,设直线![]() 的解析式为
的解析式为![]() ,把A(0,8),E(8,0)代入
,把A(0,8),E(8,0)代入
得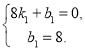
解得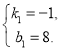 ,
,
∴直线![]() 的解析式为
的解析式为![]() 或
或![]() .
.
(3)当点F在线段OA上时,FA=BD=4,
∴OF=4,即点F的坐标为(0,4),
当点F在线段OA的延长线上时,FA=BD=4,
∴OF=12,即点F的坐标为(0,12),
当点F在线段BC右侧、AB∥DF时,DF=AB=12,
∴点F的坐标为(24,4),
综上所述,以A,D,B,F为顶点的四边形为平行四边形时,点F的坐标为(0,4)或(0,12)或(24,4).


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全国人民每天都很关心新型冠状病毒感染肺炎的全国疫情和湖北疫情,下面是2020年2月7日小明在网上看到的2020年2月6日有关全国和武汉的疫情统计图表:
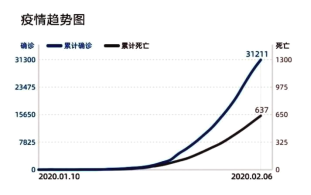
图1全国疫情趋势图
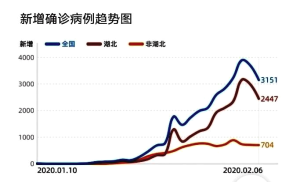
图2新增确诊病例趋势图
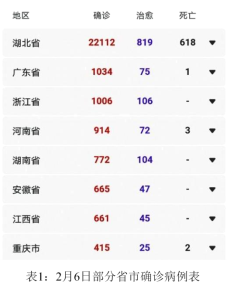
根据统计图表提供的信息,下列推断不合理的是( )
A.从图1可得出在2月6日的全国确诊病例达到3万多,是“非典”确诊病例(共5327例)的若干倍,说明新型冠状病毒比“非典”病毒传染性强.
B.从图2可得出在2月6日新增病例出现下降,说明此时全国的累计确诊病例开始下降,肺炎疫情得到控制,政府和人民的防疫工作有了显著成效
C.从图2在2月6日新增病例出现下降,可以估计2月6日后全国新型冠状病毒肺炎累计确诊病例的单日增长率会低于10%.
D.从表1可看出确诊病例较多的省市大部分都是在湖北周围,很大原因是由于携带病毒的流动人口造成的,所以控制疫情的有效手段是在家隔离,同时也可以推断在新疆和甘肃等西北地区疫情相对缓和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=![]() ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
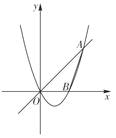
(1)求抛物线的解析式;
(2)将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,该抛物线对称轴上是否存在点
,该抛物线对称轴上是否存在点![]() ,使
,使![]() 有最小值?若存在,请求出点
有最小值?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月19日,中欧(厦门-西安-布达佩斯)班列驶出厦门自贸区海沧火车站,经西安直达匈牙利首都布达佩斯 ,我市与欧洲各国经贸往来日益频繁,某欧洲客商准备在厦门采购一批特色商品,经调查,用![]() 元采购
元采购![]() 型商品的件数是用
型商品的件数是用![]() 元采购
元采购![]() 型商品件数的
型商品件数的![]() 倍,一件
倍,一件![]() 型商品的进价比一件
型商品的进价比一件![]() 型商品的进价多
型商品的进价多![]() 元.
元.
(1)求一件![]() 型商品的进价分别为多少元?
型商品的进价分别为多少元?
(2)若该欧洲客商购进![]() 型商品共
型商品共![]() 件进行试销,其中
件进行试销,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型商品的件数,且不小于
型商品的件数,且不小于![]() 件,已知
件,已知![]() 型商品的售价为
型商品的售价为![]() 元/件,
元/件,![]() 型商品的售价为
型商品的售价为![]() 元/件,且全部售出,设购进
元/件,且全部售出,设购进![]() 型商品
型商品![]() 件.
件.
①求该客商销售这批商品的利润![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
②若欧洲商决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元,求该客商售完所有商品并捐献资金后获得的最大收益.
元,求该客商售完所有商品并捐献资金后获得的最大收益.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐徐州号高铁A与复兴号高铁B前往北京.已知A车的平均速度比B车的平均速度慢70km/n,A车的行驶时间比B车的行驶时间多25%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() ,直线
,直线![]() ,当
,当![]() 任取一值时,
任取一值时,![]() 对应的函数值分别 为
对应的函数值分别 为![]() ,若
,若![]() ,取
,取![]() 中的较小值记为
中的较小值记为![]() ;若
;若![]() ,记
,记![]() ,例如:当
,例如:当![]() 时,
时,![]() ,此时
,此时![]() ,下列判断:
,下列判断:
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() 值越大,
值越大,![]() 值越小;
值越小;
③使得![]() 大于2的
大于2的![]() 值不存在;
值不存在;
④使得![]() 的
的![]() 值是
值是![]() 或
或![]() .
.
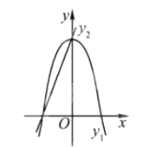
其中正确的是_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
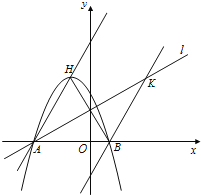
【题目】如图,抛物线y=mx![]() +2mx-3m(m≠0)的顶点为H,与
+2mx-3m(m≠0)的顶点为H,与![]() 轴交于A、B两点(B点在A点右侧),点H、B关于直线l:
轴交于A、B两点(B点在A点右侧),点H、B关于直线l:![]() 对称,过点B作直线BK∥AH交直线l于K点.
对称,过点B作直线BK∥AH交直线l于K点.
(1)求A、B两点坐标,并证明点A在直线I上。
(2)求此抛物线的解析式;
(3)将此抛物线向上平移,当抛物线经过K点时,设顶点为N,求出NK的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com