
【题目】如图,已知抛物线![]() ,直线
,直线![]() ,当
,当![]() 任取一值时,
任取一值时,![]() 对应的函数值分别 为
对应的函数值分别 为![]() ,若
,若![]() ,取
,取![]() 中的较小值记为
中的较小值记为![]() ;若
;若![]() ,记
,记![]() ,例如:当
,例如:当![]() 时,
时,![]() ,此时
,此时![]() ,下列判断:
,下列判断:
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() 值越大,
值越大,![]() 值越小;
值越小;
③使得![]() 大于2的
大于2的![]() 值不存在;
值不存在;
④使得![]() 的
的![]() 值是
值是![]() 或
或![]() .
.
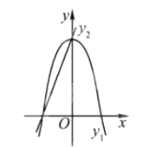
其中正确的是_______________________.
【答案】③④
【解析】
根据二次函数和一次函数的图像与性质即可得出答案.
由题可得,函数图像如图所示
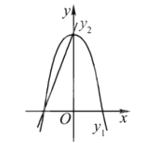
![]()
∴当-1<x<0时,![]() ;当x=-1时,
;当x=-1时,![]() ;当x<-1时,
;当x<-1时,![]() ,故①错误;
,故①错误;
由①可知,当x<0时,抛物线与直线的交点坐标为(-1,0)
结合图示,可知,当-1<x<0时,M=![]() ,当x越大时,M越大;当x=-1时,M=
,当x越大时,M越大;当x=-1时,M=![]() ;当x<-1时,M=
;当x<-1时,M=![]() ,当x越大时,M越大,故②错误;
,当x越大时,M越大,故②错误;
由以上分析可知,当x≥0时,![]() ,则M=
,则M=![]() ,此时
,此时![]() ,故
,故![]() ;当-1<x<0时,M=
;当-1<x<0时,M=![]() ,解得0<M<2;当x≤-1时,M=
,解得0<M<2;当x≤-1时,M=![]() ,解得M≤0,故③正确;
,解得M≤0,故③正确;
由③可得M=1的情况有两种:(1)当x≥0时,即![]() ,解得x=
,解得x=![]() ;(2)当-1<x<0时,2x+2=1,解得x=
;(2)当-1<x<0时,2x+2=1,解得x=![]() ,故④正确;
,故④正确;
故答案为③④.


科目:初中数学 来源: 题型:
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形![]() 如图放置在平面直角坐标系中,
如图放置在平面直角坐标系中,![]() 为边
为边![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() ,且
,且![]() ,
,![]() 的长是方程
的长是方程![]() 的两个实数根,且
的两个实数根,且![]() .
.
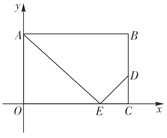
(1)设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系(不求
的函数关系(不求![]() 的取值范围);
的取值范围);
(2)当![]() 为
为![]() 的中点时,求直线
的中点时,求直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,平面内是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形?若存在,请直接写出点
为顶点的四边形为平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宣和中学图书馆今日购进甲、乙两种图书,每本甲种图书的进价比每本乙种图书的进价高20元,花780元购进甲种图书的数量与花540元购进乙种图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元;
(2)宣和中学购进甲、乙两种图书共70本,总购书费用不超过3950元,则最多购进甲种图书多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有1200名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:

(Ⅰ)本次参加跳绳测试的学生人数为___________,图①中![]() 的值为___________;
的值为___________;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级跳绳测试中得3分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的高,且
的高,且![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,点E在AD上,连接![]() ,将
,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若BE=BC,求
,若BE=BC,求![]() 的大小;
的大小;
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
图1.  图2.
图2.  图3.
图3. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组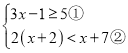
请结合题意,完成本题的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则.”
阅读下列两则材料,回答问题
材料一:平方运算和开方运算是互逆运算,如:a2±2ab+b2=(a±b)2,那么![]() =|a±b|,那么如何将双重二次根式
=|a±b|,那么如何将双重二次根式![]() (a>0,b>0,a±2
(a>0,b>0,a±2![]() >0)化简呢?如能找到两个数m,n(m>0,n>0),使得(
>0)化简呢?如能找到两个数m,n(m>0,n>0),使得(![]() 2+(
2+(![]() )2=a即m+n=a,且使
)2=a即m+n=a,且使![]() 即mn=b,那么a±2
即mn=b,那么a±2![]() =(
=(![]() )2+(
)2+(![]() )2±2
)2±2![]() =(
=(![]() 2
2
∴![]() =
=![]() =
=![]() |,双重二次根式得以化简.
|,双重二次根式得以化简.
例如化简:![]() .∵3=1+2且2=1×2,∴3+2
.∵3=1+2且2=1×2,∴3+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() ,
,
∴![]() =
=![]() =1+
=1+![]() .
.
材料二:在直角坐标系xoy中,对于点P(x,y)和Q(x,y′)出如下定义:若y′=![]() ,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
,则称点Q为点P的“横负纵变点”例如,点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5)
问题:
(1)请直接写出点(﹣3![]() ,﹣2)的“横负纵变点”为 ;化简
,﹣2)的“横负纵变点”为 ;化简![]() = ;
= ;
(2)点M为一次函数y=﹣x+1图象上的点,M′为点M的横负纵变点,已知N(1,1),若M′N=![]() ,求点M的坐标;
,求点M的坐标;
(3)已知b为常数且1≤b≤2,点P在函数y=﹣x2+16(![]() +)(
+)(![]() ﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
﹣7≤x≤a)的图象上,其“横负纵变点”的纵坐标y′的取值范围是﹣32<y′≤32,若a为偶数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com