
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

【答案】(1)EC=2![]() ;(2)证明见解析;(3)2
;(2)证明见解析;(3)2
【解析】
(1)如图1,连接对角线BD,先证明△ABD是等边三角形,根据E是AB的中点,由等腰三角形三线合一得:DE⊥AB,利用勾股定理依次求DE和EC的长;
(2)如图2,作辅助线,构建全等三角形,先证明△ADH是等边三角形,再由△AMN是等边三角形,得条件证明△ANH≌△AMD(SAS),则HN=DM,根据DQ是△CHN的中位线,得HN=2DQ,由等量代换可得结论.
(3)先判断出点N在CD的延长线上时,CN+DM最小,最小为CH,再判断出∠ACD=30°,即可用三角函数求出结论.
(1)如图1,连接BD,则BD平分∠ABC,

∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A+∠ABC=180,
∵∠A=60,
∴∠ABC=120,
∴ABD是等边三角形,
∴BD=AD=4,
∵E是AB的中点,
由勾股定理得:DE=2![]() ,
,
∵DC∥AB,
∴∠EDC=∠DEA=90,
在RtDEC中,
EC=2![]()
(2)如图2,延长CD至H,使CD=DH,连接NH、AH,
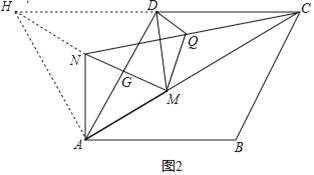
∵AD=CD,
∴AD=DH,
∵CD∥AB,
∴∠HDA=∠BAD=60,
∴ADH是等边三角形,
∴AH=AD, ∠HAD=60,
∵AMN是等边三角形,
∴AM=AN, ∠NAM=60,
∴∠HAN=∠DAM,
∴ANH≌AMD,
∴HN=DM,
∵D是CH的中点,Q是NC的中点,
∴DQ是CHN的中位线,
∴HN=2DQ,
∴DM=2DQ
(3) 如图2,由(2)知,HN=DM,
∴要CN+DM最小,便是CN+HN最小,
即:点C,H,N在同一条线上时,CN+DM最小,
此时,点D和点Q重合,
即:CN+DM的最小值为CH,
如图3,
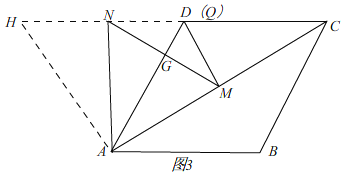
由(2)知,△ADH是等边三角形,
∴∠H=60°.
∵AC是菱形ABCD的对角线,
∴∠ACD=![]() ∠BCD=
∠BCD=![]() ∠BAD=30°,
∠BAD=30°,
∴∠CAH=180°-30°-60°=90°,
在Rt△ACH中,CH=![]() =2,
=2,
∴DM+CN的最小值为2.


科目:初中数学 来源: 题型:
【题目】如图①,直线y=-![]() x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
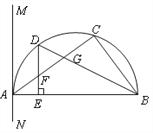
【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(1,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备销售甲、乙两种商品共80件,已知甲种商品进货价为每件70元,乙种商品进货价为每件35元,在定价销售时,2件甲种商品与3件乙种商品的售价相同,3件甲种商品比2件乙商品的售价多150元.
(1)每件甲商品与每件乙商品的售价分别是多少元?
(2)若甲、乙两种商品的进货总投入不超过4200元,则至多进货甲商品多少件?
(3)若这批商品全部售完,该商店至少盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的角平分线交AC于D,BD=4![]() ,过点C作CE⊥BD交BD的延长线于E,则CE的长为( )
,过点C作CE⊥BD交BD的延长线于E,则CE的长为( )

A.![]() B.2
B.2![]() C.3
C.3![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
(1)求直线OA和二次函数的解析式;
(2)当点P在直线OA的上方时,
①当PC的长最大时,求点P的坐标;
②当S△PCO=S△CDO时,求点P的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com