
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的角平分线交AC于D,BD=4![]() ,过点C作CE⊥BD交BD的延长线于E,则CE的长为( )
,过点C作CE⊥BD交BD的延长线于E,则CE的长为( )

A.![]() B.2
B.2![]() C.3
C.3![]() D.2
D.2![]()
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.

(1)如图1,当点E在AB边得中点位置时:
①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是 .
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ,请证明你的猜想.
(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王上周五在股市上以收盘价(收市时的价格)每股25元买进某公司股票1 000股,在接下来的一周交易日内,小王记下该股票每日收盘价相比前一天的涨跌情况:(单位:元)

根据上表回答问题:
(1)星期二收盘时,该股票每股______元.
(2)本周内股票收盘时的最高价______元.
(3)已知买入股票与卖出股票均需支付成交金额的千分之五的交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所知道的四边形中是勾股四边形的两种图形的名称_____,_____;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°后得到△DBE,连接AD、DC,若∠DCB=30°,试证明;DC2+BC2=AC2.(即四边形ABCD是勾股四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三点A(-1,1),B(-3,2),C(-4,-1).

(1)作出与△ABC关于原点对称的△A1B1C1,并写出各顶点的坐标;
(2)作出与△ABC关于P(1,-2)点对称的△A2B2C2,并写出各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
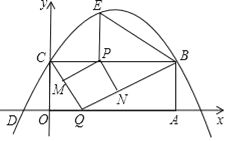
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com