
����Ŀ����ͼ��ʾ���ı���ABCD�������Σ�M��AB�ӳ�����һ�㣮ֱ�����dzߵ�һ��ֱ�DZ߾�����D����ֱ�Ƕ���E��AB���ϻ�������E�����A��B�غϣ�����һֱ�DZ�����CBM��ƽ����BF�ཻ�ڵ�F��

��1����ͼ1������E��AB�ߵ��е�λ��ʱ��
��ͨ������DE��EF�ij��ȣ�����DE��EF�����������ϵ�� ��
�����ӵ�E��AD�ߵ��е�N������NE��BF�����������ϵ�� ����֤����IJ��룮
��2����ͼ2������E��AB���ϵ�����λ��ʱ�������ʱDE��EF��������������ϵ����֤����IJ��룮
���𰸡���1����DE=EF����NE=BF�����ɼ���������2��DE=EF�����ɼ�����.
�������������������1�����������ε����ʼ�N��E�ֱ�ΪAD��AB���е�ɵ�DN=EB���ٸ��ݽ�ƽ���ߵ����ʼ�AN=AE�ɵá�DNE=��EBF=135�㣬�Ӷ���֤�á�DNE�ա�EBF���̶�֤�ý��ۣ�
��2����DA���Ͻ�ȡDN=EB������NE����N��ʹ��NE=BF��������DN=EB�ɵ�AN=AE�����ݽ�ƽ���ߵ����ʿɵá�DNE=��EBF=90��+45��=135�㣬ͨ��֤��DNE�ա�EBF���Ӷ��ý���.
��1����DE=EF����NE=BF���������£�
���ı���ABCDΪ�����Σ���AD=AB����DAB=��ABC=90�㣬��N��E�ֱ�ΪAD��AB�е㣬
��AN=DN=![]() AD��AE=EB=
AD��AE=EB=![]() AB����DN=BE��AN=AE���ߡ�DEF=90�㣬���AED+��FEB=90�㣬
AB����DN=BE��AN=AE���ߡ�DEF=90�㣬���AED+��FEB=90�㣬
�֡ߡ�ADE+��AED=90�㣬���FEB=��ADE���֡�AN=AE�����ANE=��AEN���֡ߡ�A=90�����ANE=45�㣬���DNE=180�㩁��ANE=135�㣬�֡ߡ�CBM=90�㣬BFƽ�֡�CBM��
���CBF=45�㣬��EBF=135�㣬�ڡ�DNE�͡�EBF��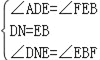 �� ���DNE�ա�EBF��ASA������DE=EF��NE=BF��
�� ���DNE�ա�EBF��ASA������DE=EF��NE=BF��
��2��DE=EF���������£�
��DA���Ͻ�ȡDN=EB������NE�����ı���ABCD�������Σ�DN=EB����AN=AE�����AENΪ����ֱ�������Σ����ANE=45�㣬���DNE=180�㩁45��=135�㣬��BFƽ�֡�CBM��AN=AE�����EBF=90��+45��=135�㣬���DNE=��EBF�� �ߡ�NDE+��DEA=90�㣬��BEF+��DEA=90�㣬���NDE=��BEF���ڡ�DNE�͡�EBF��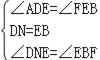 �����DNE�ա�EBF��ASA���� ��DE=EF��
�����DNE�ա�EBF��ASA���� ��DE=EF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�Ƕ�֪��![]() ��ʾ5��(-2)֮��ľ���ֵ,Ҳ������Ϊ5��-2���������������Ե�����֮��ľ���,��̽��:
��ʾ5��(-2)֮��ľ���ֵ,Ҳ������Ϊ5��-2���������������Ե�����֮��ľ���,��̽��:
(1) ��![]() = ;
= ;
(2) ʹ��![]() =3���������� ;
=3���������� ;
(3) ������̽������,�����κ�������x,��![]() ��Сֵ�� ;
��Сֵ�� ;
(4)������̽������,ʹ��![]() �ij���������x��
�ij���������x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��![]() ��
��
��2��![]() ��
��
��3����-36������+12��-��-4������-0.5����
��4����1-![]() +
+![]() ������-48����
������-48����
��5��![]() ��
��
��6��![]() ��
��
��7��![]() ��
��
��8��18��42��(��2)��(��3)2��5��
��9��![]() ��[��32��(��
��[��32��(��![]() )2��(��2)3] ��
)2��(��2)3] ��
��10��![]() ��
��
��11��![]()
��12��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ֱ��y����![]() x��3��x���ཻ�ڵ�A����y���ཻ�ڵ�B����C(m��n)�ǵڶ�������һ�㣬�Ե�CΪԲ�ĵ�Բ��x�������ڵ�E����ֱ��AB�����ڵ�F.
x��3��x���ཻ�ڵ�A����y���ཻ�ڵ�B����C(m��n)�ǵڶ�������һ�㣬�Ե�CΪԲ�ĵ�Բ��x�������ڵ�E����ֱ��AB�����ڵ�F.
(1)���ı���OBCE�Ǿ���ʱ�����C�����ꣻ
(2)��ͼ�ڣ�����C��y�������ڵ�D�����C�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ���˶���
���˶���![]() ����
����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ����
����![]() ��
��![]() ���߶�
���߶�![]() ��
��![]() .
.


��1����![]() ʱ��
ʱ��![]() = ��
= ��![]() = ����
= ����![]() ��
��![]() ��
��![]() �˶�ʱ��
�˶�ʱ��![]() �� ������������������С������
�� ������������������������
��2����![]() ���ڶ���ʱ��
���ڶ���ʱ��![]() ����˵�����ɣ�
����˵�����ɣ�
��3���ڵ�![]() ���˶������У�
���˶������У�![]() ����״�����ǵ����������������ԣ���ֱ��д��
����״�����ǵ����������������ԣ���ֱ��д��![]() �Ķ���.�������ԣ���˵������.
�Ķ���.�������ԣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�� ![]() ��
�� ![]() ����
����![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת
����ʱ�뷽����ת![]() �õ�
�õ�![]() ��
��

��1���߶�![]() �ij��� ��
�ij��� �� ![]() �Ķ����� ��
�Ķ����� ��
��2������![]() ����֤���ı���
����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��3�����ı���![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=a![]() ��4x+c��ͼ����A�͵�B��
��4x+c��ͼ����A�͵�B��

��1����ö��κ����ı���ʽ��
��2��д���������ߵĶԳ��ἰ�������ꣻ
��3����P��m��m�����Q���ڸú���ͼ���ϣ�����m��0��������������������ߵĶԳ���Գƣ���m��ֵ����Q��x��ľ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
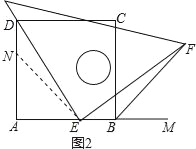
����Ŀ����ͼ����ABC�ڽ��ڰ�Բ��AB��ֱ������A��ֱ��MN������MAC����ABC��
��1����֤��MN�ǰ�Բ�����ߣ�
��2����D�ǻ�AC���е㣬����BD��AC ��G����D��DE��AB��E����AC��F����֤��FD��FG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A��90����AB��AC����ABC�Ľ�ƽ���߽�AC��D��BD��4![]() ������C��CE��BD��BD���ӳ�����E����CE�ij�Ϊ��������
������C��CE��BD��BD���ӳ�����E����CE�ij�Ϊ��������

A.![]() B.2
B.2![]() C.3
C.3![]() D.2
D.2![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com