
【题目】不览夜景,未到重庆山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,![]() 小时后一快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为
小时后一快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为![]()
![]() ,快艇和轮船之间的距离为
,快艇和轮船之间的距离为![]() ,
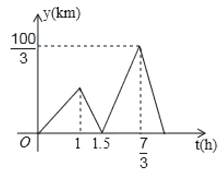
,![]() 与
与![]() 的函数关系式如图所示,则快艇与轮船第二次相遇时到朝天门码头的距离为_____千米.
的函数关系式如图所示,则快艇与轮船第二次相遇时到朝天门码头的距离为_____千米.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐徐州号高铁A与复兴号高铁B前往北京.已知A车的平均速度比B车的平均速度慢70km/n,A车的行驶时间比B车的行驶时间多25%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
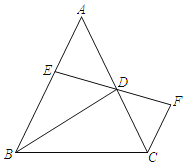
【题目】已知:如图,在△ABC中AB=AC,BD平分∠ABC交AC于点D,DE平分∠ADB交AB于点E,CF∥AB交ED的延长线于F,若∠A=52°,求∠DFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
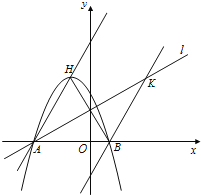
【题目】如图,抛物线y=mx![]() +2mx-3m(m≠0)的顶点为H,与
+2mx-3m(m≠0)的顶点为H,与![]() 轴交于A、B两点(B点在A点右侧),点H、B关于直线l:
轴交于A、B两点(B点在A点右侧),点H、B关于直线l:![]() 对称,过点B作直线BK∥AH交直线l于K点.
对称,过点B作直线BK∥AH交直线l于K点.
(1)求A、B两点坐标,并证明点A在直线I上。
(2)求此抛物线的解析式;
(3)将此抛物线向上平移,当抛物线经过K点时,设顶点为N,求出NK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
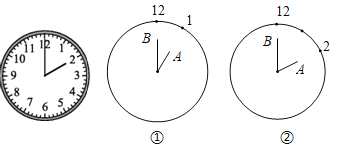
【题目】如图,有一时钟,时针OA长为6cm,分针OB长为8cm,△OAB随着时间的变化不停地改变形状.求:
(1)如图①,13点时,△OAB的面积是多少?
(2)如图②,14点时,△OAB的面积比13点时增大了还是减少了?为什么?
(3)问多少整点时,△OAB的面积最大?最大面积是多少?请说明理由.
(4)设∠BOA=α(0°≤α≤180°),试归纳α变化时△OAB的面积有何变化规律(不证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]()
![]() 的图象与性质.因为
的图象与性质.因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
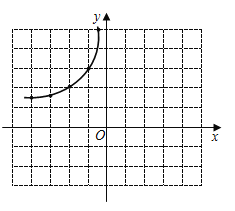
(1)请补全函数图象;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而_________;(填“增大”或“减小”)
的增大而_________;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向________平移________个单位而得到;
的图象向________平移________个单位而得到;
③图象关于点_________中心对称.(填点的坐标)
(3)结合函数图象,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
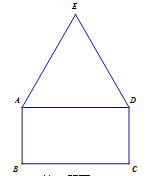
【题目】如图所示,矩形ABCD的边长AB=2,BC=2![]() ,△ADE为正三角形.
,△ADE为正三角形.
若半径为R的圆能够覆盖五边形ABCDE(即五边形ABCDE的每个顶点都在圆内或圆上),则R的最小值是( )
A.2![]() B.4C.2.8D.2.5
B.4C.2.8D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
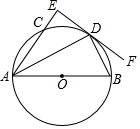
【题目】如图,在⊙O中,AB是直径,点C是圆上一点,点D是弧BC中点,过点D作⊙O切线DF,连接AC并延长交DF于点E.
(1)求证:AE⊥EF;
(2)若圆的半径为5,BD=6 求AE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com