
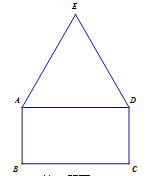
【题目】如图所示,矩形ABCD的边长AB=2,BC=2![]() ,△ADE为正三角形.
,△ADE为正三角形.
若半径为R的圆能够覆盖五边形ABCDE(即五边形ABCDE的每个顶点都在圆内或圆上),则R的最小值是( )
A.2![]() B.4C.2.8D.2.5
B.4C.2.8D.2.5
【答案】C
【解析】
连接AC、BE、CE,取BC的中点F,连接EF,根据勾股定理可得AC,根据直角三角形的边角关系可得∠ACB=30°,∠CAD=30°,再根据正三角形的性质可得:∠EAD=∠EDA=60°,AE=AD=DE=2![]() ,进而推出△EAC是直角三角形,由勾股定理可得EC的长.判断△EAB≌△EDC,根据全等三角形的性质可得EB=EC,继而根据题意可判断能够覆盖五边形ABCDE的最小圆的圆心在线段EF上,且此圆只要覆盖住△EBC必能覆盖五边形ABCDE,从而此圆的圆心到△BCE的三个顶点距离相等.根据等腰三角形的判定和性质可得F是BC中点,BF=CF=
,进而推出△EAC是直角三角形,由勾股定理可得EC的长.判断△EAB≌△EDC,根据全等三角形的性质可得EB=EC,继而根据题意可判断能够覆盖五边形ABCDE的最小圆的圆心在线段EF上,且此圆只要覆盖住△EBC必能覆盖五边形ABCDE,从而此圆的圆心到△BCE的三个顶点距离相等.根据等腰三角形的判定和性质可得F是BC中点,BF=CF=![]() ,EF⊥BC,由勾股定理可得EF的长,继而列出关于R的一元二次方程,解方程即可解答.
,EF⊥BC,由勾股定理可得EF的长,继而列出关于R的一元二次方程,解方程即可解答.
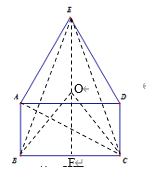
如图所示,连接AC、BE、CE,取BC的中点F,连接EF,
∵四边形ABCD是矩形,
∴∠ABC=∠DAB=∠BCD=∠ADC=90°,AD∥BC,AD=BC=2![]() ,AB=CD=2
,AB=CD=2
∵BC=2![]() ,AB=2
,AB=2
由勾股定理可得:
AC=![]() =
=![]() =4
=4
∴sin∠ACB=![]() =
=![]() ,sin∠CAD=
,sin∠CAD=![]() =
=![]()
∴∠ACB=30°,∠CAD=30°
∵△ADE是正三角形
∴∠EAD=∠EDA=60°,AE=AD=DE=2![]() ,
,
∴∠EAC=∠EAD+∠CAD=90°,
∴△EAC是直角三角形,
由勾股定理可得:
EC=![]() =
=![]() =
=![]()
∵∠EAB=∠EAD+∠BAD=150°
∠EDC=∠EDA+∠ADC=150°
∴∠EAB=∠EDC
∵EA=ED,AB=DC
∴△EAB≌△EDC
∴EB=EC=![]()
即△EBC是等腰三角形
∵五边形ABCDE是轴对称图形,其对称轴是直线EF,
∴能够覆盖五边形ABCDE的最小圆的圆心在线段EF上,且此圆只要覆盖住△EBC必能覆盖五边形ABCDE.从而此圆的圆心到△BCE的三个顶点距离相等.
设此圆圆心为O,则OE=OB=OC=R,
∵F是BC中点
∴BF=CF=![]() ,EF⊥BC
,EF⊥BC
在Rt△BEF中,由勾股定理可得:
EF=![]() =
=![]() =5
=5
∴OF=EF-OE=5-R
在Rt△OBF中,![]()
即![]()
解得:R=2.8
∴能够覆盖五边形ABCDE的最小圆的半径为2.8.
故选C.


科目:初中数学 来源: 题型:
【题目】解不等式组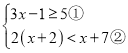
请结合题意,完成本题的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不览夜景,未到重庆山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,![]() 小时后一快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为
小时后一快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为![]()
![]() ,快艇和轮船之间的距离为
,快艇和轮船之间的距离为![]() ,
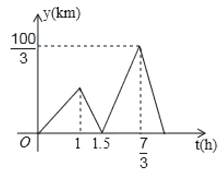
,![]() 与
与![]() 的函数关系式如图所示,则快艇与轮船第二次相遇时到朝天门码头的距离为_____千米.
的函数关系式如图所示,则快艇与轮船第二次相遇时到朝天门码头的距离为_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形![]() 是平行四边形.
是平行四边形.
求作:菱形![]() (点
(点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上).
上).
作法:①以![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;
;
②以![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;
;
③连接![]() .所以四边形
.所以四边形![]() 为所求作的菱形.
为所求作的菱形.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() ,
,![]() ,
,
∴ = .
在![]() 中,
中,![]() .
.
即![]() .
.
∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() ,
,
∴四边形![]() 为菱形( )(填推理的依据).
为菱形( )(填推理的依据).

查看答案和解析>>
科目:初中数学 来源: 题型:
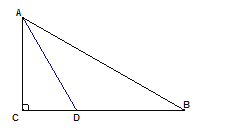
【题目】已知,如图,在Rt△ABC中,∠C=90,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心作⊙O,使它过A,D两点(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=3![]() ,BD=3,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和
,BD=3,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数![]() 的
的![]() 的部分对应值:
的部分对应值:
| ··· |
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
| ··· |
则对于该函数的性质的判断:
①该二次函数有最小值;
②不等式![]() 的解集是
的解集是![]() 或
或![]()
③方程![]() 的实数根分别位于
的实数根分别位于![]() 和
和![]() 之间;
之间;
④当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;
的增大而增大;
其中正确的是:
A.①②③B.②③C.①②D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
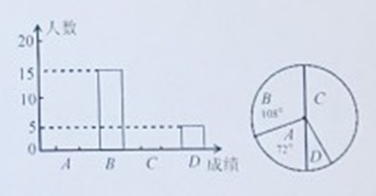
【题目】某校九年级体自模拟测试后,随机抽取了九年级部分学生体有测试成绩进行统计,得到相关的统计图表如下:
成绩/分 |
|
|
|
|
成绩等级 |
|
|
|
|
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的体育测试成绩,补全频数分布直方图
(2)扇形![]() 的圆心角的度数是
的圆心角的度数是
(3)若该校九年级有![]() 名学生,请据此估计该校九年级此次体育测试成绩在
名学生,请据此估计该校九年级此次体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生有多少人?
等级)的学生有多少人?
(4)根据测试中存在的问题,通过一段时间的针对性调练,若![]() 等级学生数可提高
等级学生数可提高![]() 等级学生数可提高
等级学生数可提高![]() ,请估计经过训练后九年级体育测试成绩在
,请估计经过训练后九年级体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生可达多少人?
等级)的学生可达多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
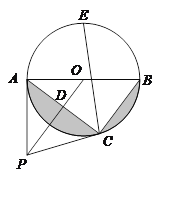
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com