
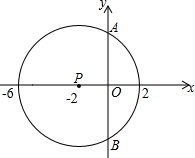
 如图,已知⊙P的圆心为P(-2,0),与x轴有公共点(-6,0),(2,0).
如图,已知⊙P的圆心为P(-2,0),与x轴有公共点(-6,0),(2,0).分析 (1)∵由点P坐标得出OP=2,由⊙P与x轴有公共点(-6,0),(2,0),得出⊙P的半径为6-2=4;
(2)连接PA、PB,由勾股定理求出OA=2$\sqrt{3}$,同理:OB=2$\sqrt{3}$,即可得出结果.
解答 解:(1)∵P(-2,0),
∴OP=2,
∵⊙P与x轴有公共点(-6,0),(2,0),
∴⊙P的半径为6-2=4;
(2)连接PA、PB,如图所示: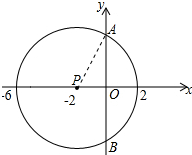
由勾股定理得:OA=$\sqrt{P{A}^{2}-O{P}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
同理:OB=2$\sqrt{3}$,
∴点A(0,2$\sqrt{3}$),点B(0,-2$\sqrt{3}$).
点评 本题考查了垂径定理、坐标与图形性质、勾股定理;熟练掌握坐标与图形性质,运用勾股定理求出OA是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com