
【题目】解不等式(3x+4)(3x﹣4)﹣x(x﹣4)>8(x+1)2 , 并把它的解集在数轴上表示出来. ![]()
【答案】解:9x2﹣16﹣x2+4x>8x2+16x+8, 12x<﹣24,
解得x<﹣2,
把它的解集在数轴上表示为,![]()
【解析】根据平方差公式、完全平方公式先展开,再计算,求得不等式的解集,再表示在数轴上即可.
【考点精析】解答此题的关键在于理解不等式的解集在数轴上的表示的相关知识,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈,以及对一元一次不等式的解法的理解,了解步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题).


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】两个三角形是通过平移得到的,下列说法错误的是( )
A. 平移过程中,两三角形周长不变
B. 平移过程中,两三角形面积不变
C. 平移过程中,两三角形的对应线段一定相等
D. 平移过程中,两三角形的对应边必平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.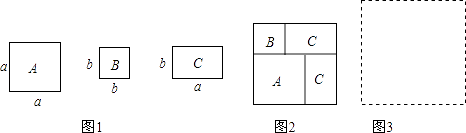
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是 , 并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
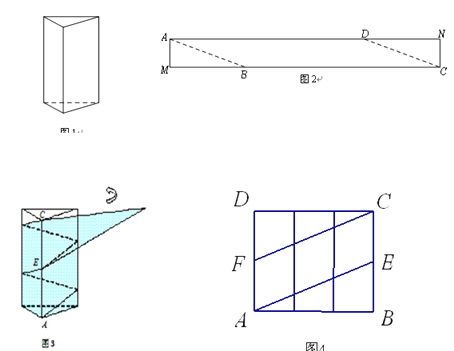
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
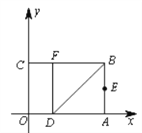
【题目】如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=70°,AC=BC , 以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′B′C , 点A′恰好落在AC上,连接CC′,则∠ACC′=.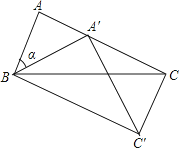
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com