
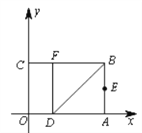
ΓΨΧβΡΩΓΩ»γΆΦ,“‘ΨΊ–ΈOABCΒΡΕΞΒψOΈΣ‘≠Βψ,OAΥυ‘ΎΒΡ÷±œΏΈΣx÷α,OCΥυ‘ΎΒΡ÷±œΏΈΣy÷α,Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒ.“―÷ΣOA=3,OC=2,ΒψE «ABΒΡ÷–Βψ,‘ΎOA…œ»Γ“ΜΒψD,ΫΪΓςBDA―ΊBDΖ≠’έΘ§ ΙΒψA¬δ‘ΎBC±Ώ…œΒΡΒψF¥ΠΘ°
Θ®1Θ©÷±Ϋ”–¥≥ωΒψEΓΔFΒΡΉχ±ξΘΜ
Θ®2Θ©…ηΕΞΒψΈΣFΒΡ≈ΉΈοœΏΫΜy÷α’ΐΑκ÷α”ΎΒψP,«““‘ΒψEΓΔFΓΔPΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ§«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©‘Ύx÷αΓΔy÷α…œ «ΖώΖ÷±π¥φ‘ΎΒψMΓΔN, ΙΒΟΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–ΓΘΩ»γΙϊ¥φ‘Ύ,«σ≥ω÷ή≥ΛΒΡΉν–Γ÷ΒΘΜ»γΙϊ≤Μ¥φ‘Ύ,«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©E(3Θ§1),F(1Θ§2);Θ®2Θ©![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§Ήν–ΓΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–Γ÷Β «5+
ΘΜΘ®3Θ©¥φ‘ΎΘ§Ήν–ΓΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–Γ÷Β «5+![]() Θ°
Θ°
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©ΓςBDA―ΊBDΖ≠’έΘ§ ΙΒψA¬δ‘ΎBC±Ώ…œΒΡΒψF¥ΠΘ§Ω…“‘÷ΣΒάΥΡ±Ώ–ΈADFB «’ΐΖΫ–ΈΘ§“ρΕχBF=AB=OC=2Θ§‘ρCF=3-2=1Θ§“ρΕχEΓΔFΒΡΉχ±ξΨΆΩ…“‘«σ≥ωΘ°Θ®2Θ©ΕΞΒψΈΣFΒΡΉχ±ξΗυΨίΒΎ“ΜΈ Ω…“‘«σΒΟ «Θ®1Θ§2Θ©Θ§“ρΕχ≈ΉΈοœΏΒΡΫβΈω ΫΩ…“‘…ηΈΣy=aΘ®x-1Θ©2+2Θ§“‘ΒψEΓΔFΓΔPΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ§”ΠΖ÷EF «―ϋΚΆΒΉ±ΏΝΫ÷÷«ιΩωΫχ––Χ÷¬έΘ°
ΔΌΒ±EF «―ϋΘ§EF=PF ±Θ§“―÷ΣEΓΔFΒψΒΡΉχ±ξΩ…“‘«σ≥ωEFΒΡ≥ΛΘ§…ηPΒψΒΡΉχ±ξ «Θ®0Θ§nΘ©Θ§ΗυΨίΙ¥Ι…Ε®άμΨΆΩ…“‘«σ≥ωnΒΡ÷ΒΘ°ΒΟΒΫPΒΡΉχ±ξΘ°Β±EF «―ϋΘ§EF=EP ±Θ§Ω…“‘≈–ΕœEΒΫy÷αΒΡΉνΕΧΨύάκ”κEFΒΡ¥σ–ΓΙΊœΒΘ§÷Μ”–Β±EF¥σ”ΎEΒΫy÷αΒΡΨύάκΘ§P≤≈¥φ‘ΎΘ°
ΔΎΒ±EF «ΒΉ±Ώ ±Θ§EP=FPΘ§ΗυΨίΙ¥Ι…Ε®άμΨΆΩ…“‘ΒΟΒΫΙΊ”ΎnΒΡΖΫ≥ΧΘ§ΨΆΩ…“‘ΫβΒΟnΒΡ÷ΒΘ°
Θ®3Θ©ΉςΒψEΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψEΓδΘ§ΉςΒψFΙΊ”Ύy÷αΒΡΕ‘≥ΤΒψFΓδΘ§Ν§Ϋ”EΓδFΓδΘ§Ζ÷±π”κx÷αΓΔy÷αΫΜ”ΎΒψMΘ§NΘ§‘ρΒψMΘ§NΨΆ «Υυ«σΒψΘ°«σ≥ωœΏΕΈEΓδFΓδΒΡ≥ΛΕ»Θ§ΨΆ «ΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΒΡΉν–Γ÷ΒΘ°
±ΨΧβΫβΈωΘΚ(1)E(3,1);F(1,2).
(2)‘ΎRtΓςEBF÷–,ΓœB=90Θ§ΓύEF=![]()
…ηΒψPΒΡΉχ±ξΈΣ(0,n)Θ§Τδ÷–n>0Θ§ΓΏΕΞΒψF(1,2)Θ§
Γύ…η≈ΉΈοœΏΫβΈω ΫΈΣy=a(x1) ![]() +2(aΓΌ0).
+2(aΓΌ0).
ΔΌ»γΆΦ1Θ§
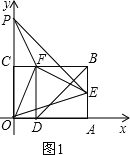 Β±EF=PF ±,
Β±EF=PF ±, ![]() Θ§
Θ§
Γύ![]() .
.
ΫβΒΟ![]() (…α»Ξ);
(…α»Ξ); ![]() .
.
ΓύP(0,4).
Γύ4=a(01) ![]() +2.
+2.
ΫβΒΟa=2.
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=2(x1) ![]() +2
+2
ΔΎ»γΆΦ2Θ§
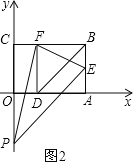
Β±EP=FP ±,EP![]() =FP
=FP![]() Θ§Γύ(2n)
Θ§Γύ(2n) ![]() +1=(1n)
+1=(1n) ![]() +9.ΫβΒΟ
+9.ΫβΒΟ![]() (…α»Ξ)
(…α»Ξ)
ΔέΒ±EF=EP ±,EP=![]() <3Θ§’β÷÷«ιΩω≤Μ¥φ‘ΎΓΘ
<3Θ§’β÷÷«ιΩω≤Μ¥φ‘ΎΓΘ
Ήέ…œΥυ ω,ΖϊΚœΧθΦΰΒΡ≈ΉΈοœΏΫβΈω Ϋ «y=2(x1) ![]() +2.
+2.
(3)¥φ‘ΎΒψM,N, ΙΒΟΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–ΓΓΘ
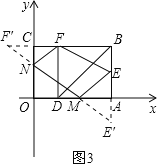
»γΆΦ3,ΉςΒψEΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψEΓδ,ΉςΒψFΙΊ”Ύy÷αΒΡΕ‘≥ΤΒψFΓδΘ§
Ν§Ϋ”EΓδFΓδΘ§Ζ÷±π”κx÷αΓΔy÷αΫΜ”ΎΒψMΘ§NΘ§‘ρΒψMΘ§NΨΆ «Υυ«σΒψΓΘ
ΓύEΓδ(3,1),FΓδ(1,2),NF=NFΓδ,ME=MEΓδ.ΓύBFΓδ=4,BEΓδ=3.
ΓύFN+NM+ME=FΓδN+NM+MEΓδ=EΓδFΓδ=![]() .
.
”÷ΓΏEF=![]() Θ§
Θ§
ΓύFN+MN+ME+EF=5+![]() ,¥Υ ±ΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–Γ÷Β «5+
,¥Υ ±ΥΡ±Ώ–ΈMNFEΒΡ÷ή≥ΛΉν–Γ÷Β «5+![]() .
.


 ΦΛΜνΥΦΈ§”≈Φ”ΩΈΧΟœΒΝ–¥πΑΗ
ΦΛΜνΥΦΈ§”≈Φ”ΩΈΧΟœΒΝ–¥πΑΗ ΜνΝΠ ‘ΨμœΒΝ–¥πΑΗ
ΜνΝΠ ‘ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΜ·ΦρΘΚ
Θ®1Θ©3m2©¹5m2©¹m2
Θ®2Θ©©¹3xy©¹2y2+5xy©¹4y2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫβ≤ΜΒ» ΫΘ®3x+4Θ©Θ®3x©¹4Θ©©¹xΘ®x©¹4Θ©ΘΨ8Θ®x+1Θ©2 Θ§ ≤ΔΑ―ΥϋΒΡΫβΦ·‘Ύ ΐ÷α…œ±μ Ψ≥ωά¥Θ° ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2-2x+m=0”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§‘ρ Β ΐmΒΡ»Γ÷ΒΖΕΈßΈΣ________
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫβ≤ΜΒ» ΫΉι  Α―ΥϋΒΡΫβΦ·±μ Ψ‘Ύ ΐ÷α…œΘ§≤Δ«σ≥ω≤ΜΒ» ΫΉιΒΡΖ«ΗΚ’ϊ ΐΫβΘ°
Α―ΥϋΒΡΫβΦ·±μ Ψ‘Ύ ΐ÷α…œΘ§≤Δ«σ≥ω≤ΜΒ» ΫΉιΒΡΖ«ΗΚ’ϊ ΐΫβΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§ΓœB=60ΓψΘ§BC=2Θ°ΫΪΓςABC»ΤΒψCΥ≥ ±’κ–ΐΉΣΒΟΒΫΓςAΓδBΓδC Θ§ Ν§ΫαABΓδΘ°»τAΓΔBΓδΓΔAΓδ‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§‘ρAAΓδΒΡ≥ΛΈΣΘ®ΓΓΓΓΘ©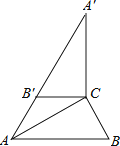
A.6
B.![]()
C.![]()
D.3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§ΓœACB=90ΓψΘ§AC=BCΘ§÷±œΏMNΨ≠ΙΐΒψCΘ§«“ADΓΆMN”ΎDΘ§BEΓΆMN”ΎEΘ° 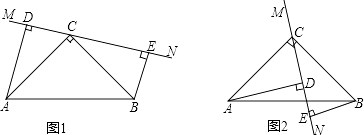
Θ®1Θ©Β±÷±œΏMN»ΤΒψC–ΐΉΣΒΫΆΦ1ΒΡΈΜ÷Ο ±Θ§ «σ÷ΛΘΚΔΌΓςADCΓ’ΓςCEBΘΜΔΎDE=AD+BEΘΜ
Θ®2Θ©Β±÷±œΏMN»ΤΒψC–ΐΉΣΒΫΆΦ2ΒΡΈΜ÷Ο ±Θ§Θ®1Θ©÷–ΒΡΫα¬έΜΙ≥…ΝΔ¬πΘΩ»τ≥…ΝΔΘ§«κΗχ≥ω÷ΛΟςΘΜ»τ≤Μ≥…ΝΔΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§œ÷“Σάϊ”Ο≥ΏΙφΉςΆΦΉςΓςABCΙΊ”ΎBCΒΡ÷αΕ‘≥ΤΆΦ–ΈΓςAΓδBC Θ° »τABΘΫ5cm Θ§ ACΘΫ6cm Θ§ BCΘΫ7cm Θ§ ‘ρΖ÷±π“‘ΒψBΓΔCΈΣ‘≤–ΡΘ§“ά¥Έ“‘cmΓΔcmΈΣΑκΨΕΜ≠ΜΓΘ§ ΙΒΟΝΫΜΓœύΫΜ”ΎΒψAΓδ Θ§ ‘ΌΝ§ΫαAΓδCΓΔAΓδB Θ§ Φ¥Ω…ΒΟΓςAΓδBC Θ° 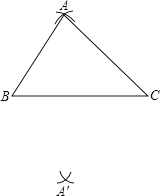
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com