
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E. 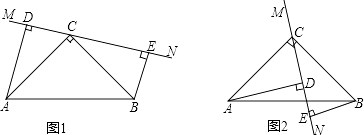
(1)当直线MN绕点C旋转到图1的位置时, 求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
【答案】
(1)证明:①∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,
∴∠DAC=∠BCE.
又AC=BC,∠ADC=∠BEC=90°,
∴△ADC≌△CEB.
②∵△ADC≌△CEB,
∴CD=BE,AD=CE.
∴DE=CE+CD=AD+BE
(2)△ADC≌△CEB成立,DE=AD+BE.不成立,此时应有DE=AD﹣BE.
证明:∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,
∴∠DAC=∠BCE.
又AC=BC,∠ADC=∠BEC=90°,
∴△ADC≌△CEB.
∴CD=BE,AD=CE.
∴DE=AD﹣BE
【解析】(1)直角三角形中斜边对应相等,即可证明全等,再由线段对应相等,得出②中结论;(2)由图可知,△ADC与△CEB仍全等,但线段的关系已发生改变.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
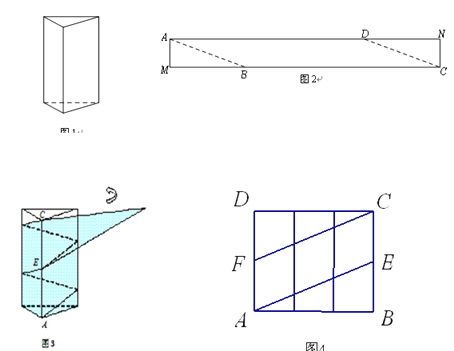
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
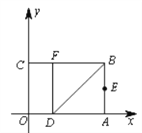
【题目】如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算中正确的是( )
A. (x+2)2=x2+2x+4 B. (-3-x)(3+x)=9-x2
C. (-3-x)(3+x)=-x2-9+6x D. (2x-3y)2=4x2+9y2-12xy
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=70°,AC=BC , 以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′B′C , 点A′恰好落在AC上,连接CC′,则∠ACC′=.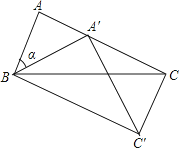
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查显示,2016年“两会”期间,通过手机等移动端设备对“两会”相关话题的浏览量高达115 000 000次.将115 000 000 用科学记数法表示应为( )
A.1.15×109
B.11.5×107
C.1.15×108
D.1.158
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com