
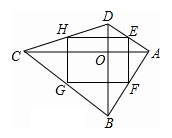
 .则下列结论:①△AFD≌△AEB;②点B到直线AE的距离为
.则下列结论:①△AFD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△AFD+S△AFB=1+
;③EB⊥ED;④S△AFD+S△AFB=1+ ;⑤S正方形ABCD =4+
;⑤S正方形ABCD =4+ .其中正确结论的序号是 ( )
.其中正确结论的序号是 ( )
| A.①③④ | B.①②⑤ | C.③④⑤ | D.①③⑤ |
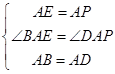 ,
, AE=
AE= ,
, ,
,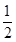 ×1×1+
×1×1+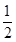 ×
× ×2,
×2, ,故④正确;
,故④正确;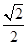 ×2=
×2= ,
, ,故②错误,
,故②错误,

科目:初中数学 来源:不详 题型:解答题
 ,如图1所示,将△
,如图1所示,将△ 的顶点
的顶点 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A( ),B在同一条直线上,如图2所示,观察图2可知:旋转角
),B在同一条直线上,如图2所示,观察图2可知:旋转角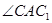 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。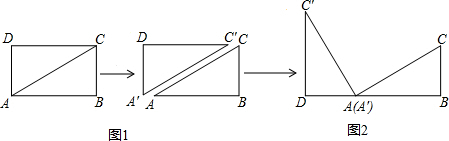

 ,连接
,连接 ,求
,求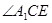 的度数。
的度数。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com