
【题目】如图,已知点A是双曲线y= ![]() 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y=
在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y= ![]() 上运动,则k的值是 .
上运动,则k的值是 . 
【答案】﹣3 ![]()
【解析】解:设A(a, ![]() ),
),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC= ![]() AO,
AO,
∵AO= ![]() ,
,
∴CO= ![]() ,
,
如图,过点C作CD⊥x轴于点D,则可得∠AOD=∠OCD(都是∠COD的余角),

设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,
即 ![]() =
= ![]() ,
,
解得y=﹣ ![]() a2x.
a2x.
在Rt△COD中,CD2+OD2=OC2,
即y2+x2=3a2+ ![]() ,
,
将y=﹣ ![]() a2x代入,可得:
a2x代入,可得:
x2= ![]() ,
,
故x= ![]() ,y=﹣
,y=﹣ ![]() a,
a,
则xy=﹣3 ![]() ,即k=﹣3
,即k=﹣3 ![]() .
.
所以答案是:﹣3 ![]() .
.
【考点精析】利用反比例函数的性质和等边三角形的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;等边三角形的三个角都相等并且每个角都是60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连结BF.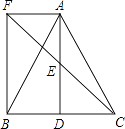
(1)求证:①△EAF≌△EDC;
②D是BC的中点;
(2)若AB=AC,求证:四边形AFBD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
![]() 如图1,点E为BC上一点,点F为AC上一点,且
如图1,点E为BC上一点,点F为AC上一点,且![]() ,连接AE,BF交于点G,求
,连接AE,BF交于点G,求![]() 的度数;
的度数;
![]() 如图2,点M是BC延长线上一点,
如图2,点M是BC延长线上一点,![]() ,MN交
,MN交![]() 的外角平分线于点N,求
的外角平分线于点N,求![]() 的值;
的值;
![]() 如图3,过点A作
如图3,过点A作![]() 于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边
于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边![]() ,连DQ,则DQ的最小值是______.
,连DQ,则DQ的最小值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=3,则BC长为( )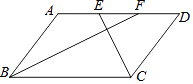
A.9
B.10
C.11
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】穿越青海境内的兰新高速铁路正在加紧施工.某工程队承包了一段全长1957米的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5米,经过6天施工,甲、乙两组共掘进57米.
(1)求甲乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天比原来多掘进0.3米,乙组平均每天比原来多掘进0.2米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.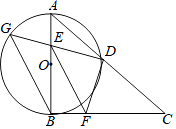
(1)求证:AE=BF.
(2)连接GB,EF,求证:GB∥EF.
(3)若AE=1,EB=3,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线ABCDE描述了一辆汽车在某一直线上行驶过程中,汽车离出发地的距离y(km)和行驶时间x(h)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120km;②汽车在行驶途中停留了0.5h;③汽车在整个行驶过程中的平均速度为![]() km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)
km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.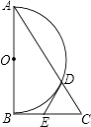
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com