
����Ŀ����ͼ���ھ���ABCD�У�AB=1cm��AD=3cm����Q��A���������1cm/s���ٶ���AD���յ�D�˶�����P�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶���������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶�������ͬʱ�������˶���t��.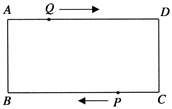
��1����0��t��3���ж��ı���BQDP����״����˵��������
��2�����ı���BQDP������S���˶�ʱ��t�ĺ�����ϵʽ��
��3������tΪ��ֵʱ���ı���BQDPΪ����.
���𰸡�
��1���⣺���ı���ABCD�Ǿ��Σ���AD//BC.
�ߵ�Q�ӵ�A��������1cm/s���ٶ���AD���յ�D�˶���
ͬʱ����P�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶���
��QD=BP��
���ı���BPDQ��ƽ���ı���
��2���⣺��BP=9-t�����ı���BQDP�����S=BPAB=��3-t����1=3-t=-t+3
��3���⣺��һ���ڱ���ȵ�ƽ���ı��������Σ���BQ=PQ.
��AQ=t��AB=1�� ![]() ,QD=3-t
,QD=3-t
![]()
��֮�� ![]()
����������1�����ı���ABCD�Ǿ��Σ��õ��Ա�AD//BC����Q�ӵ�A��������1cm/s���ٶ���AD���յ�D�˶���ͬʱ����P�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶����õ�QD=BP������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��õ�BPDQ��ƽ���ı��Σ���2����BP=9-t���õ��ı���BQDP�����S=BPAB���õ��ı���BQDP������S���˶�ʱ��t�ĺ�����ϵʽ����3����һ���ڱ���ȵ�ƽ���ı��������Σ���֪BQ=PQ���������εĶԽ����ഹֱƽ�֣��ٸ��ݹ��ɶ��������BQ�Ĵ���ʽ����QD=3-t�����t��ֵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽�����֡�
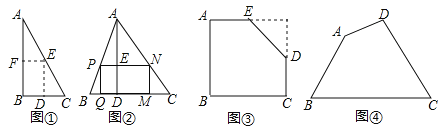
��ͼ������һ��ֱ��������ֽƬ����B=60�㣬С������м���һ������BΪ�ڽ���������ľ��Σ�������β������֣���������λ��DE��EF����ʱ�����õľ��ε������������ͨ��֤����֤������ȷ�ԣ����ó������ε���������ԭ����������ı�ֵΪ ��
����չӦ�á�
��ͼ��������ABC�У�BC=a��BC���ϵĸ�AD=h������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵΪ �����ú�a��h�Ĵ���ʽ��ʾ��
�����Ӧ�á�
��ͼ������һ�顰ȱ�Ǿ��Ρ�ABCDE��AB=32��BC=40��AE=20��CD=16��С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
��ʵ��Ӧ�á�
��ͼ��������һ���ı��ε�ľ������ABCD��������AB=50cm��BC=108cm��CD=60cm����tanB=tanC=![]() ��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ֽƬ![]() �У�
�У�![]() �DZ�
�DZ�![]() �ϵĵ㣬��ֽƬ��
�ϵĵ㣬��ֽƬ��![]() �۵���ʹ��
�۵���ʹ��![]() ���ڵ�
���ڵ�![]() ��������
��������![]() ����
����![]() Ϊֱ��������ʱ��
Ϊֱ��������ʱ��![]() �ij�Ϊ___________��
�ij�Ϊ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a3a2=a6
B.��a2��2=a4
C.����3a��3=��9a3
D.a4+a5=a9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������ǣ� ��
A.��� ![]() =1����ôa=1��
=1����ôa=1��
B.�����ڽǷֱ��Ӧ��ȵ�����������ȫ�ȣ�
C.���a������������ôa��ʵ�� ��
D.����һ�Ƕ�Ӧ��ȵ�����������ȫ�ȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���P����3��5������x��ĶԳƵ�������ǣ�������
A. ��3����5�� B. ����3����5�� C. ��3��5�� D. ��5����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�͡�ADE���ǵȱ�������.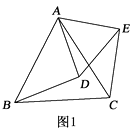
��1����֤��BD=CE��
��2����ͼ2����BD���е�ΪP �� CE���е�ΪQ �� ���жϡ�APQ����״����˵������.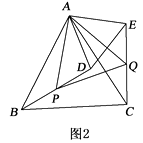
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У������ж���ֱ��������ȫ�ȵ��ǣ� ��
A. б�ߺ�һ��Ƕ�Ӧ���
B. б���ϵ����ߺ�һֱ�DZ߶�Ӧ���
C. ���߷ֱ����
D. ֱ�ǵ�ƽ���ߺ�һֱ�DZ߶�Ӧ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com