
【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成如图所示的不完整的统计图表,请根据图表中的信息解答下列问题:
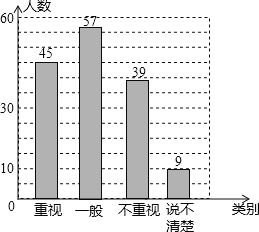
某校初中生阅读数学教科书情况统计图表

类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图.
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数.
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
【答案】(1)150人, 如图所示见解析;(2)598人;(3)①同学们应重视阅读数学教科书,从而获取更多的数学课外知识和对相关习题、定理的深层次理解与认识,②应随机抽取不同的学校以及不同的年级进行抽样,进而分析.
【解析】
(1)利用类别为“一般”人数与所占百分比,进而得出样本容量,进而得出a,b,c的值;
(2)利用“不重视阅读数学教科书”在样本中所占比例,进而估计全校在这一类别的人数;
(3)根据(1)中所求数据进而分析得出答案,再从样本抽出的随机性进而得出答案.
(1)由题意可得出:样本容量为:57÷0.38=150(人),
∴a=150×0.3=45,
b=150-57-45-9=39,
c=39÷150=0.26,
如图所示:
(2)若该校共有初中生2300名,
该校“不重视阅读数学教科书”的初中人数约为:2300×0.26=598(人);
(3)①根据以上所求可得出:只有30%的学生重视阅读数学教科书,有32%的学生不重视阅读数学教科书或说不清楚,可以看出大部分学生忽略了阅读数学教科书,同学们应重视阅读数学教科书,从而获取更多的数学课外知识和对相关习题、定理的深层次理解与认识.
②如果要了解全省初中生阅读数学教科书的情况,应随机抽取不同的学校以及不同的年级进行抽样,进而分析.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果对于某一特定范围内的x的任意允许值,P=|10﹣2x|+|10﹣3x|+|10﹣4x|+|10﹣5x|+…+|10﹣10x|为定值,则此定值是( )
A. 20 B. 30 C. 40 D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.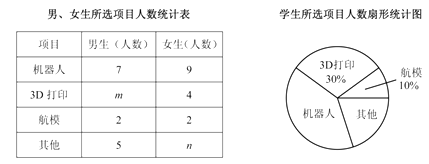
根据以上信息解决下列问题:
(1)![]() ,
, ![]() ;
;![]()
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的 ![]() 名学生中随机选取
名学生中随机选取 ![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的 ![]() 名学生中恰好有
名学生中恰好有 ![]() 名男生、
名男生、 ![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设购买甲种树苗x棵,有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x的式子表示);
树苗类型 | 甲种树苗 | 乙种树苗 |
购买树苗数量(单位:棵) | x | |
购买树苗的总费用(单位:元) |
②如果购买甲、乙两种树苗共用去25 600元,那么甲、乙两种树苗各购买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26 000元,求n的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是BC的中点
,点D是BC的中点![]() 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
![]() 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;
![]() 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转![]() ,
,
![]() 判断
判断![]() 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论;
![]() 若
若![]() ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
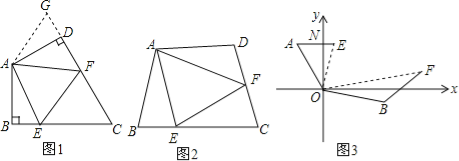
【题目】(13分)(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
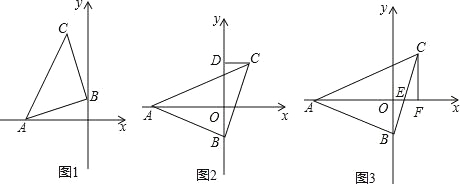
【题目】已知,△ABC 是等腰直角三角形,BC=AB,A 点在 x 负半轴上,直角顶点 B 在 y 轴上,点 C 在 x 轴上方.
(1)如图1所示,若A的坐标是(﹣3,0),点 B的坐标是(0,1),求点 C 的坐标;
(2)如图2,过点 C 作 CD⊥y 轴于 D,请直接写出线段OA,OD,CD之间等量关系;
(3)如图3,若 x 轴恰好平分∠BAC,BC与 x 轴交于点 E,过点 C作 CF⊥x 轴于 F,问 CF 与 AE 有怎样的数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com