
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
【答案】(1)见解析;(2) 直角三角形;(3) 125°或110°或140°
【解析】试题分析:
(1) 根据题意可知,△BOC通过旋转变换得到△ADC. 根据旋转变换的性质可知,△BOC≌△ADC. 由此易知,△COD是等腰三角形. 根据上述旋转变换的旋转角可知,∠OCD=60°. 不难证明等腰三角形COD为等边三角形.
(2) 结合第(1)小题的结论可知,∠ODC=60°. 根据旋转变换的性质可知,∠BOC=∠ADC=α=150°. 不难发现,∠ADO=90°. 这可以说明△AOD是直角三角形. 进一步观察图形可知,共用顶点O的四个角组成一个周角,可以利用这一关系求得∠AOD的度数,进而利用三角形内角和求得∠OAD的度数. △AOD的形状可以用这三个内角的度数进行描述.
(3) 由于△AOD的三个内角两两相等均可以使△AOD为等腰三角形,所以应该对这三个内角两两相等的三种情况分别进行讨论. 在讨论之前,应该先求得这三个内角与α的关系,这样可以将两个内角相等的条件转化为关于α的方程,进而求得符合条件的α的值. 根据第(2)小题的思路可知,利用“共用顶点O的四个角组成一个周角”这一关系,可以得到∠AOD与α的关系式;利用旋转变换的性质和等边三角形的性质,可以得到∠ADO与α的关系式;在△AOD中利用三角形内角和可以得到∠OAD与α的关系式. 在求得这些关系式后,依照上述的解题思路进行分情况讨论即可.
试题解析:
(1) 证明:
∵△BOC绕点C旋转得到△ADC,
∴△BOC≌△ADC,
∴OC=DC,
∵△BOC绕点C按顺时针方向旋转60°得到△ADC,
∴∠OCD=60°,
∴△COD是等边三角形.
(2) △AOD是两个锐角分别为40°和50°的直角三角形. 理由如下.
∵△COD是等边三角形,
∴∠COD=∠ODC=60°,
∵△BOC≌△ADC,
又∵α=150°,
∴∠BOC=∠ADC=α=150°.
∴∠ADO=∠ADC-∠ODC=150°-60°=90°,
∴△AOD是直角三角形.
∵∠AOB+∠BOC+∠COD+∠AOD=360°
又∵∠AOB=110°,∠BOC=α=150°,∠COD=60°,
∴∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-150°-60°=40°,
∴在Rt△AOD中,∠OAD=90°-∠AOD=90°-40°=50°.
∴△AOD是两个锐角分别为40°和50°的直角三角形.
(3) ∵△COD是等边三角形,
∴∠COD=∠CDO=60°.
∵∠AOB=110°,∠COD=60°,
∴∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-α-60°=190°-α.
∵∠BOC=∠ADC=α,
∴∠ADO=∠ADC-∠CDO=α-60°.
∴在△AOD中,∠OAD=180°-∠AOD-∠ADO=180°-(190°-α)-(α-60°)=50°.
根据题意,△AOD的三个内角两两相等均可以使△AOD为等腰三角形,
故应该对下面三种情况分别进行讨论.
①若∠ADO=∠AOD,即α-60°=190°-α,∴α=125°.
②若∠ADO=∠OAD,即α-60°=50°,∴α=110°.
③若∠OAD=∠AOD,即50°=190°-α,∴α=140°.
综上所述,当α为125°或110°或140°时,△AOD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
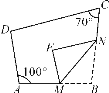
A. 115° B. 105° C. 95° D. 85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD交于点E,DF⊥AC于F点,若∠ADF=3∠FDC,则∠DEC的度数是( )
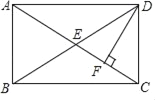
A. 30° B. 45° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
(2)【类比探究】
如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(3)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是一元二次方程2x2﹣2x+1﹣3m=0的两个实数根,且x1、x2满足不等式x1x2+2(x1+x2)>0,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,
x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,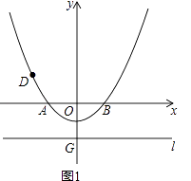
(1)求抛物线对应的二次函数的解析式;
(2)若D为抛物线y= ![]() x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
(3)如图2,若E、F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.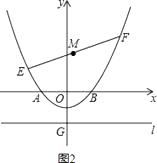
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
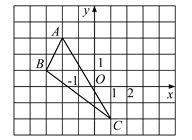
【题目】(1)如图,在平面直角坐标系中,请画出△ABC关于y轴对称的△A′B′C′,并写出A′,B′,C′三点的坐标;(其中A′,B′,C′分别是A,B,C的对应点,不写画法)
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com