
����Ŀ�������
��1�������������
��ͼ�٣���֪��ABC�ǵ��������Σ���E���߶�AB�ϣ���D��ֱ��BC�ϣ���ED=EC������BCE�Ƶ�C˳ʱ����ת60������ACF����EF
��֤����AB=DB+AF
��2�������̽����
��ͼ�ڣ������E���߶�AB���ӳ����ϣ������������䣬�߶�AB��DB��AF֮������������������ϵ����˵������
��3�������E���߶�BA���ӳ����ϣ������������䣬����ͼ�۵Ļ����Ͻ�ͼ�β�����������д��AB��DB��AF֮���������ϵ������˵�����ɣ�
���𰸡�
��1��
֤����ED=EC=CF��
�ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF��
���ECF=60�㣬��BCA=60�㣬BE=AF��EC=CF��
���CEF�ǵȱ������Σ�
��EF=EC����CEF=60�㣬
�֡�ED=EC��
��ED=EF��
�ߡ�ABC�ǵ��������Σ���BCA=60�㣬
���ABC�ǵȱ������Σ�
���CAF=��CBA=60�㣬
���EAF=��BAC+��CAF=120�㣬��DBE=120�㣬��EAF=��DBE��
�ߡ�CAF=��CEF=60�㣬
��A��E��C��F�ĵ㹲Բ��
���AEF=��ACF��
�֡�ED=EC��
���D=��BCE����BCE=��ACF��
���D=��AEF��
�ڡ�EDB�͡�FEA�У�
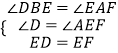 ��AAS��
��AAS��
���EDB�ա�FEA��
��DB=AE��BE=AF��
��AB=AE+BE��
��AB=DB+AF
��2��
֤����AB=BD��AF��
�ӳ�EF��CA���ڵ�G��
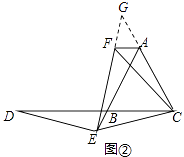
�ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF��
���ECF=60�㣬BE=AF��EC=CF��
���CEF�ǵȱ������Σ�
��EF=EC��
�֡�ED=EC��
��ED=EF����EFC=��BAC=60�㣬
�ߡ�EFC=��FGC+��FCG����BAC=��FGC+��FEA��
���FCG=��FEA��
�֡ߡ�FCG=��ECD����D=��ECD��
���D=��FEA��
����ת�����ʣ��ɵ�
��CBE=��CAF=120�㣬
���DBE=��FAE=60�㣬
�ڡ�EDB�͡�FEA�У�
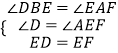 ��AAS��
��AAS��
���EDB�ա�FEA��
��BD=AE��EB=AF��
��BD=FA+AB��
��AB=BD��AF
��3��
֤������ͼ�ۣ�
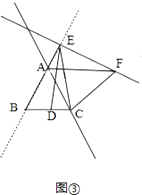 ��
��
ED=EC=CF��
�ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF��
���ECF=60�㣬BE=AF��EC=CF��BC=AC��
���CEF�ǵȱ������Σ�
��EF=EC��
�֡�ED=EC��
��ED=EF��
��AB=AC��BC=AC��
���ABC�ǵȱ������Σ�
���ABC=60�㣬
�֡ߡ�CBE=��CAF��
���CAF=60�㣬
���EAF=180�㩁��CAF����BAC
=180�㩁60�㩁60��
=60��
���DBE=��EAF��
��ED=EC��
���ECD=��EDC��
���BDE=��ECD+��DEC=��EDC+��DEC��
�֡ߡ�EDC=��EBC+��BED��
���BDE=��EBC+��BED+��DEC=60��+��BEC��
�ߡ�AEF=��CEF+��BEC=60��+��BEC��
���BDE=��AEF��
�ڡ�EDB�͡�FEA�У�
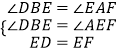 ��AAS��
��AAS��
���EDB�ա�FEA��
��BD=AE��EB=AF��
��BE=AB+AE��
��AF=AB+BD��
��AB��DB��AF֮���������ϵ�ǣ�
AF=AB+BD
����������1�������жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬���ԡ�EAF=��BAC+��CAF=120�㣬��DBE=120�㣬��EAF=��DBE��Ȼ�����ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��AB=AE+BF������AB=DB+AF����2�������жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬���ԡ�EFC=��FGC+��FCG����BAC=��FGC+��FEA����FCG=��FEA���ٸ��ݡ�FCG=��EAD����D=��EAD���ɵá�D=��FEA��Ȼ�����ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��EB=AF�������жϳ�AB=BD��AF���ɣ���3�����ȸ��ݵ�E���߶�BA���ӳ����ϣ���ͼ�۵Ļ����Ͻ�ͼ�β���������Ȼ���жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬���жϳ���DBE=��EAF����BDE=��AEF��������ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��EB=AF�������жϳ�AF=AB+BD���ɣ�
�����㾫�������ڱ��⿼��ĵȱ������ε����ʣ���Ҫ�˽�ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60����ܵó���ȷ�𰸣�


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB�ǡ�O��ֱ������C�� ![]() ���е㣬��COB=60�㣬����C��CE��AD����AD���ӳ����ڵ�E
���е㣬��COB=60�㣬����C��CE��AD����AD���ӳ����ڵ�E 
��1����֤��CEΪ��O�����ߣ�
��2���ж��ı���AOCD�Ƿ�Ϊ���Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������2500ֻ�����������.���������ȡ��һ���ּ����������ǵ���������λ��![]() �������Ƴ����µ�ͳ��ͼ�ٺ�ͼ��.����������Ϣ������������⣺
�������Ƴ����µ�ͳ��ͼ�ٺ�ͼ��.����������Ϣ������������⣺

������ͼ����![]() ��ֵΪ ��
��ֵΪ ��
������ͳ�Ƶ��������ݵ�ƽ��������������λ����
���� �����������ݣ�������2500ֻ���У�����Ϊ![]() ��Լ�ж���ֻ��
��Լ�ж���ֻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣���Գ�����x=��1���ҹ��㣨��3��0��������˵������abc��0����2a��b=0����4a+2b+c��0����������5��y1������ ![]() ��y2���������������㣬��y1��y2 �� ����˵����ȷ���ǣ� ��
��y2���������������㣬��y1��y2 �� ����˵����ȷ���ǣ� �� 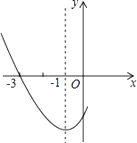
A.�٢�
B.�ڢ�
C.�٢ڢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA����2��1����B����4��5����C����5��2����
��1���ٻ�����ABC����y��ԳƵġ�A1B1C1��
�ڻ�����ABC����ԭ��O�����ĶԳƵġ�A2B2C2��
��2�����A2B2C2�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BOC=9�㣬��A��OB�ϣ���OA=1��������Ҫ��ͼ��
��AΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A1���õ�1���߶�AA1������A1ΪԲ�ģ�1Ϊ�뾶���һ�����OB�ڵ�A2���õ�2���߶�A1A2������A2ΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A3���õ�3���߶�A2A3������������ȥ��ֱ���õ�n���߶Σ�֮��Ͳ����ٻ�������Ҫ����߶��ˣ���n=______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �ǵȱ�
�ǵȱ�![]() ��һ�㣬
��һ�㣬 ![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() ��
��![]() ������
������![]() ��
��

(1)��֤�� ![]() �ǵȱ������Σ�
�ǵȱ������Σ�
(2)��![]() ʱ�����ж�
ʱ�����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
(3)̽������![]() Ϊ���ٶ�ʱ��
Ϊ���ٶ�ʱ�� ![]() �ǵ��������Σ�
�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���B=60�����Խ���ACƽ�ֽǡ�BAD����P�ǡ�ABC��һ�㣬����PA��PB��PC����PA=6��PB=8��PC=10��������ABCD���������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4���ӳ�CB��M��ʹBM=2������AM��BN��AM��N��O��AC��BD�Ľ��㣬����ON����ON�ij�Ϊ 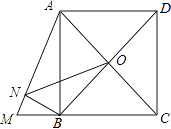
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com