
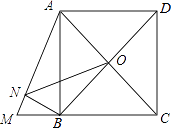
【题目】如图,正方形ABCD的边长为4,延长CB至M,使BM=2,连接AM,BN⊥AM于N,O是AC、BD的交点,连接ON,则ON的长为 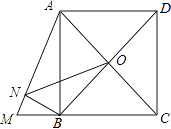
【答案】![]()
【解析】解:∵AB=4,BM=2,
∴AM= ![]() =2
=2 ![]() ,
,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN= ![]() ,MN=
,MN= ![]() ,
,
∵AB=4,CD=4,
∴AC=4 ![]() ,
,
∴AO=2 ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() ,且∠CAM=∠NAO
,且∠CAM=∠NAO
∴△AON∽△AMC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴ON= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握勾股定理的概念和正方形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】解答题
(1)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
(2)【类比探究】
如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(3)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,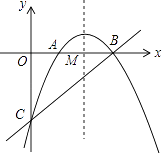
(1)求△ABC的面积;
(2)若p是x轴上方的抛物线上的一个动点,求点P到直线BC的距离的最大值;
(3)若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,求直线PC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BE于点B,DE⊥BE于点E.
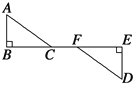
(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是____;
(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是_________;
(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是_______;
(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在出行中,主动采用能降低二氧化碳排放量的交通方式,谓之“低碳出行”.明明一家积极响应政府“绿色山城,低碳出行”的号召,今年2月﹣5月明明一家减少了驾车出行,他们将2月﹣5月驾车行驶的里程统计后绘制成以下两幅不完整的统计图: 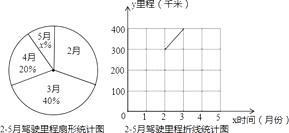
(1)扇形统计图中x= , 并补全折线统计图;
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在平面直角坐标系中,请画出△ABC关于y轴对称的△A′B′C′,并写出A′,B′,C′三点的坐标;(其中A′,B′,C′分别是A,B,C的对应点,不写画法)
(2)求△ABC的面积.
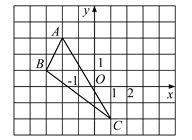
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)
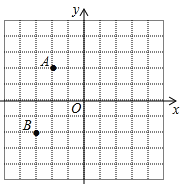
(1)若点D与点A关于y轴对称,则点D的坐标为 .
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为 .
(3)求A,B,C,D组成的四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).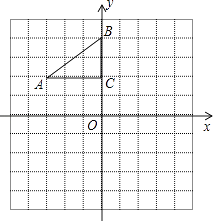
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com