
����Ŀ����֪��ͬѧ���в������ŷֱ�������� ![]() ��
�� ![]() ��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ��������1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ��������1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
��1������������ͼ���б����г����п��ܵĽ����
��2�����ƶ�һ����Ϸ��������ѡ����a��b��ʹ��ax2+bx+1=0����������ȵ�ʵ���������ʤ�������һ�ʤ��������������Ϸ����ƽ�����ø���֪ʶ���ͣ�
���𰸡�
��1���⣺����״ͼ���£�
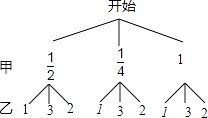
��ͼ��֪������9�ֵȿ��ܵĽ����
��2���⣺�ߣ�a��b���Ŀ��ܽ���У� ![]() ��1������
��1������ ![]() ��3������
��3������ ![]() ��2������
��2������ ![]() ��1������
��1������ ![]() ��3������
��3������ ![]() ��2������1��1������1��3������1��2����
��2������1��1������1��3������1��2����
�൱a= ![]() ��b=1ʱ����=b2��4ac=��1��0����ʱax2+bx+1=0��ʵ������
��b=1ʱ����=b2��4ac=��1��0����ʱax2+bx+1=0��ʵ������
��a= ![]() ��b=3ʱ����=b2��4ac=7��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=3ʱ����=b2��4ac=7��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a= ![]() ��b=2ʱ����=b2��4ac=2��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=2ʱ����=b2��4ac=2��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a= ![]() ��b=1ʱ����=b2��4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��b=1ʱ����=b2��4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��a= ![]() ��b=3ʱ����=b2��4ac=8��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=3ʱ����=b2��4ac=8��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a= ![]() ��b=2ʱ����=b2��4ac=3��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=2ʱ����=b2��4ac=3��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=1��b=1ʱ����=b2��4ac=��3��0����ʱax2+bx+1=0��ʵ������
��a=1��b=3ʱ����=b2��4ac=5��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=1��b=2ʱ����=b2��4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��P����ʤ��=P������0��= ![]() ��P���һ�ʤ��=1��
��P���һ�ʤ��=1�� ![]() =
= ![]() ��
��
��P����ʤ����P���һ�ʤ����
����������Ϸ����Լ�����������ƽ��
����������1�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ������2������һԪ���η��̸����б�ʽ�������ж���������¸��������Ȼ�����ø��ʹ�ʽ��⼴����üס��һ�ʤ�ĸ��ʣ��Ƚϸ��ʴ�С������ȷ����������Ϸ���Ƿ�ƽ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������Ȥ�С����Χ��һ����������������һ�߿�ǽ�����������ܳ�Ϊ30�����Χ�ɣ���֪ǽ��Ϊ18�ף���ͼ��ʾ�����ش��������⣺ 
��1�������������ֱ��ǽ��һ�ߵij�Ϊx�ף���ƽ����ǽ��һ�߳�Ϊ�����ú�x�Ĵ���ʽ��ʾ��
��2����ƽ����ǽ��һ�߳���С��8�ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=ax2+bx+c��a��0����ͼ���뺯��y=x�� ![]() ��ͼ����ͼ��ʾ�������н��ۣ���ab��0����c����
��ͼ����ͼ��ʾ�������н��ۣ���ab��0����c���� ![]() ����a+b+c����
����a+b+c���� ![]() ���ܷ���ax2+��b��1��x+c+
���ܷ���ax2+��b��1��x+c+ ![]() =0����������ȵ�ʵ������������ȷ���У� ��
=0����������ȵ�ʵ������������ȷ���У� �� 
A.4 ��
B.3 ��
C.2 ��
D.1 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD������ECGF�ı߳��ֱ�Ϊ2��4����A=120�㣮����Ӱ��������� �� ������������ţ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD�Ǹߣ�CE�����ߣ���G��CE���е㣬DG��CE����GΪ���㣮 
��1����֤��DC=BE��
��2������AEC=66�㣬���BCE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����BAC=54�㣬��ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E������B����O�����ߣ���AC���ӳ����ڵ�F�� 
��1����֤��BE=CE��
��2�����CBF�Ķ�����
��3����AB=6���� ![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��m��n����ƽ��ֱ������ϵxOy�У�x���m��y���n�������O1Ϊԭ�㣬��A ������Ϊ��1��1��������O1ƽ��2 ![]() ����λ���ȵ���O2 �� ��A��λ�ò��䣬�����O2Ϊԭ�㣬��ô��A����������ǣ� ��
����λ���ȵ���O2 �� ��A��λ�ò��䣬�����O2Ϊԭ�㣬��ô��A����������ǣ� ��
A.��3����1��
B.��1����3��
C.����2����1��
D.��2 ![]() +1��2
+1��2 ![]() +1��
+1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������һ������ε��ڽǺ�ʱ�������������һ���ڽǼ������飬������Ľ��Ϊ2004������������ڽ��Ƕ��ٶȣ����������Ǽ����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ͼ����ͬһֱ������ϵ�ڣ����κ���y=ax2+��a+c��x+c��һ�κ���y=ax+c�Ĵ���ͼ������ֻ��һ������ȷ�ģ���ȷ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com