
【题目】下列说法:①有一个角是![]() 的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
【答案】C
【解析】
根据等边三角形及等腰三角形的判定方法对各选项逐一判断即可.
当60°角是等腰三角形顶角时,两个底角为60°,三角形是等边三角形,
当60°角是底角时,顶角为60°,三角形是等边三角形,故①正确,
如图,BE为△ABC的外角平分线,且BE//AC,
∵BE//AC
∴∠A=∠EBD,∠C=∠CBE,
∵BE平分∠CBD,
∴∠CBE=∠EBD,
∴∠A=∠C,
∴AB=BC,
∴△ABC是等腰三角形,故②正确,

∵线段垂直平分线时的得到线段两端的距离相等,
∴三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;故③正确,
∵等腰三角形的两个底角相等,不一定是60°,
∴有两个角相等的等腰三角形不一定是等边三角形,故④错误,
综上所述:正确的有①②③共3个,
故选C.


科目:初中数学 来源: 题型:
【题目】市政府计划对城区道路进行改造,现安排甲、乙两个工程队共同完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造
倍,甲队改造![]() 米的道路比乙队改造同样长的道路少用
米的道路比乙队改造同样长的道路少用![]() 天.
天.
(1)甲、乙两个工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天的改造费用![]() 万元,乙队工作一天的改造费用为
万元,乙队工作一天的改造费用为![]() 万元,如需改造的道路全长为
万元,如需改造的道路全长为![]() 米,改造总费用不超过
米,改造总费用不超过![]() 万元,至少安排甲队工作多少天?
万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调 | 彩电 | |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点. 请你从以下四个关系
∠FDE=∠A 、∠BFD=∠DEC 、DE∥BA、DF∥CA中选择三个适当地填写在下面的横线上,使其形成一个真命题,并有步骤的证明这个命题(证明过程中注明推理根据).

如果 , ,
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两名工人参加操作技能培训.他们在培训期间参加的8次测试成绩记录如下表:
甲 | 73 | 82 | 70 | 85 | 80 | 70 | 75 | 65 |
乙 | 85 | 72 | 78 | 71 | 83 | 69 | 74 | 68 |
则下列说法错误的是( )
A.甲、乙的平均成绩都是75
B.甲成绩的众数是70
C.乙成绩的中位数是73
D.若从中选派一人参加操作技能比赛,从成绩稳定性考虑,应选甲
查看答案和解析>>
科目:初中数学 来源: 题型:
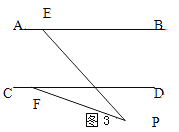
【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
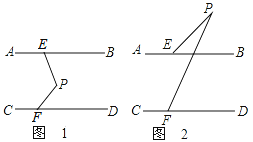
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,对角线AC、BD交于点O,且AC=16cm,BD=12cm;点P从点A出发,沿AD方向匀速运动,速度为2cm/s;点Q从点C出发,沿CO方向匀速运动,速度为1cm/s;若P、Q两点同时出发,当一个点停止运动时,另一个点也停止运动.过点Q作MQ∥BC,交BD于点M,设运动时间为t(s)(0<t<5).解答下列问题:
(1)求t为何值时,线段AQ、线段PM互相平分.
(2)设四边形APQM的面积为Scm2 , 求S关于t的函数关系式;设菱形ABCD的面积为SABCD , 求是否存在一个时刻t,使S:SABCD=2:5?如果存在,求出t,如果不存在,请说明理由.
(3)求时刻t,使得以M、P、Q为顶点的三角形是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com