
【题目】已知射线OM,ON,∠MON=45°点A在射线OM上,点B在射线ON上,OA=1,若△AOB是轴对称图形,点P为AB的中点,则OP2= .
【答案】![]() 或
或 ![]() 或
或 ![]()
【解析】解:如图所示,
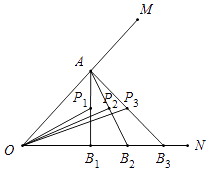
分三种情况:
①当AB1=OB1时,△AOB1是等腰直角三角形,AB1=OB1= ![]() ,
,
∴B1P1= ![]() AB1=
AB1= ![]() ×
× ![]() =
= ![]() ,
,
∴Rt△OB1P1中,OP12=OB12+B1P12=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() ;
;
②当AO=B2O时,△AOB2是等腰三角形,
Rt△AB1B2中,AB2= ![]() =
= ![]() ,
,
∵OP2⊥AB2,AB1⊥OB2,
∴ ![]() ×AB2×OP2=
×AB2×OP2= ![]() ×OB2×AB1,
×OB2×AB1,
∴OP2= ![]() =
= ![]() ,
,
∴OP22=( ![]() )2=
)2= ![]() ;
;
③当AO=AB3时,△AOB3是等腰直角三角形,
∵AP3= ![]() AB3=
AB3= ![]() ,
,
∴Rt△AOP3中,OP32=AO2+AP32=12+( ![]() )2=
)2= ![]() ;
;
综上所述,OP2= ![]() 或
或 ![]() 或
或 ![]() .
.
所以答案是: ![]() 或
或 ![]() 或
或 ![]() .
.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握轴对称图形(两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴)的相关知识才是答题的关键.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=﹣5
D.x1=﹣1,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=﹣![]() (x>0)的图象分别交BA、BC于点D、E,当BD=3AD,且△BDE的面积为18时,则k的值是_____.
(x>0)的图象分别交BA、BC于点D、E,当BD=3AD,且△BDE的面积为18时,则k的值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).动点P从点A处出发,并按A﹣B﹣C﹣D﹣A﹣B…的规律在四边形ABCD的边上以每秒1个单位长的速度运动,运动时间为t秒.若t=2018秒,则点P所在位置的点的坐标是_____.
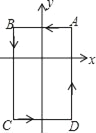
查看答案和解析>>
科目:初中数学 来源: 题型:
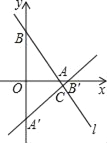
【题目】如图,在平面直角坐标系中,直线y=﹣2x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
(1)求直线A′B′所对应的函数表达式.
(2)若直线A′B′与直线AB相交于点C,求△A′BC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①有一个角是![]() 的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形BCDE为平行四边形,点A在BE的延长线上且AE=EB.连接EC,AC,AD.
(1)求证:△AED≌△EBC.
(2)若∠ACB=90°,则四边形AECD是什么特殊四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com