
【题目】如图,已知四边形BCDE为平行四边形,点A在BE的延长线上且AE=EB.连接EC,AC,AD.
(1)求证:△AED≌△EBC.
(2)若∠ACB=90°,则四边形AECD是什么特殊四边形?请说明理由.
【答案】
(1)证明:∵四边形BCDE是平行四边形,
∴ED∥BC,DE=BC,
∴∠AED=∠B,
在△AED和△EBC中,
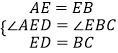 ,
,
∴△AED≌△EBC
(2)解:结论:四边形AECD是菱形.
理由:∵四边形BCDE是平行四边形,
∴AB∥CD,BE=CD,
∵AE=BE,
∴AE=CD,AE∥CD,
∴四边形AECD是平行四边形,
∵∠ACB=90°,
∴AC⊥BC,∵BC∥DE,
∴AC⊥DE,
∴四边形AECD是菱形.
【解析】(1)根据平行四边形的性质得出ED∥BC,DE=BC,进而得出∠AED=∠B,然后利用SAS判断出△AED≌△EBC;
(2)结论:四边形AECD是菱形.利用平行四边形的性质得出AB∥CD,BE=CD,进而判断出四边形AECD是平行四边形,然后根据平行线的性质得出AC⊥DE,从而得出四边形AECD是菱形.
【考点精析】本题主要考查了平行线的性质和平行四边形的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两名工人参加操作技能培训.他们在培训期间参加的8次测试成绩记录如下表:
甲 | 73 | 82 | 70 | 85 | 80 | 70 | 75 | 65 |
乙 | 85 | 72 | 78 | 71 | 83 | 69 | 74 | 68 |
则下列说法错误的是( )
A.甲、乙的平均成绩都是75
B.甲成绩的众数是70
C.乙成绩的中位数是73
D.若从中选派一人参加操作技能比赛,从成绩稳定性考虑,应选甲
查看答案和解析>>
科目:初中数学 来源: 题型:
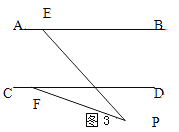
【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
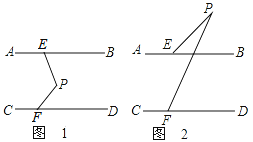
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截.红方行驶26千米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西37°方向前进,刚好在D处成功拦截蓝方.求拦截点D处到公路的距离AD.
(参考数据:sin67°≈ ![]() ,cos67°≈
,cos67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() ,sin37°≈
,sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放以来,国家经济实力和国民生活水平不断提高,但经济发展的同时对环境产生了较大的污染,环境治理已刻不容缓.某市为加快环境治理,引进新的垃圾处理设备,计划对该市2017年第一季度沿河收集的6000吨垃圾进行集中处理.
(1)写出处理完这批垃圾所用时间y(天)关于日均垃圾处理量x(吨)的函数关系式.
(2)该市垃圾实际处理过程中由于提高效能,日均垃圾处理量比原计划多20%,结果比原计划少用5天处理完全部垃圾,求原计划日均垃圾处理量为多少吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,对角线AC、BD交于点O,且AC=16cm,BD=12cm;点P从点A出发,沿AD方向匀速运动,速度为2cm/s;点Q从点C出发,沿CO方向匀速运动,速度为1cm/s;若P、Q两点同时出发,当一个点停止运动时,另一个点也停止运动.过点Q作MQ∥BC,交BD于点M,设运动时间为t(s)(0<t<5).解答下列问题:
(1)求t为何值时,线段AQ、线段PM互相平分.
(2)设四边形APQM的面积为Scm2 , 求S关于t的函数关系式;设菱形ABCD的面积为SABCD , 求是否存在一个时刻t,使S:SABCD=2:5?如果存在,求出t,如果不存在,请说明理由.
(3)求时刻t,使得以M、P、Q为顶点的三角形是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD等于( )
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com